Выкарыстанне фрэймавага падыходу ў навучанні матэматыцы дае магчымасць настаўніку стварыць для навучэнцаў сітуацыю, якая дазваляе за кароткі час самастойна асвоіць навучальны матэрыял і паспяхова прымяняць атрыманыя веды ў практычнай дзейнасці, пераносіць іх у новую жыццёвую сітуацыю.
Марына ІГНАЦІК,
настаўнік матэматыкі
ДУА “Дварэцкая сярэдняя школа”
Дзятлаўскага раёна,
Гродзенская вобласць
Сучасны ўрок каштоўны сёння стварэннем умоў для максімальнага развіцця індывідуальнасці навучэнца, здольнага самастойна працаваць з інфармацыяй, усведамляць свае дзеянні, умець аналізаваць і выкарыстоўваць веды ў розных жыццёвых сітуацыях.
Для актывізацыі гэтай самастойнасці значным становіцца вырашэнне пытання, звязанага з пошукам новых метадаў і падыходаў да арганізацыі дзейнасці навучэнцаў, якія забяспечваюць эфектыўную работу з інфармацыяй. Адным з такіх з’яўляецца фрэймавы падыход.
Выкарыстанне фрэймавага падыходу пры фарміраванні пазнавальных універсальных навучальных дзеянняў на ўроках матэматыкі можна прасачыць на прыкладзе прымянення фрэйма як мадэлі (акна, у якім змяшчаецца вызначэнне, формула, апорны канспект або кадр малюнка); фрэйма як каркаса (блок-схемы, логіка-сэнсавай матрыцы, апорна-вузлавой схемы); фрэйма як сцэнарыя (скрыпта, алгарытму, апісання).
Фрэйм як мадэль з’яўляецца другасным тэкстам, бо ў ім у кароткай форме перадаюцца асноўныя звесткі зыходнага тэксту. Пераўтварэнне навучэнцамі інфармацыі, перавод яе ў больш наглядную форму спрыяе лепшаму разуменню і засваенню ведаў. Асноўнае прызначэнне фрэйма як мадэлі складаецца ў тым, каб данесці да навучэнца логіку арганізацыі навучання, узаемасувязь тэм, якія вывучаюцца, задач курсу і іх узаемаабумоўленасць. Складанне фрэйма як мадэлі дазваляе навучэнцам за кароткі час навучыцца здабываць з тэксту інфармацыю, разумеючы сэнс прачытанага, падзяляць матэрыял на другарадны і асноўны, які павінен трывала зафіксавацца ў доўгачасовай памяці, усталёўваць узаемасувязі паміж асноўнымі змястоўнымі кампанентамі матэрыялу, абагульняць і сістэматызаваць атрыманую інфармацыю, выбіраючы галоўнае, крытычна ацэньваць і прайграваць атрыманыя вынікі.
Фрэйм як каркас выкарыстоўваецца пры вывучэнні навучальнага матэрыялу, разбітага на блокі і тэмы. Прадстаўленне вучэбнай інфармацыі ў выглядзе фрэйм-схем з наяўнымі пустымі слотамі спрыяе шматразоваму яго перазапаўненню. Пры гэтым магчыма любая форма пабудовы фрэйм-схем. Аднак трэба яе будаваць так, каб яна ўяўляла закончаную лагічную структуру. У тым выпадку, калі навучальны матэрыял дзеліцца на падтэмы, выкарыстоўваецца пастаянная каркасная структура, у якой змяняецца толькі змест слотаў у залежнасці ад заяўленай тэмы інфармацыі. Каркасная аснова выкарыстоўваецца з мэтай пабудовы логіка-сэнсавых мадэляў, якія па сваёй структуры ўяўляюць сабой фрэймавыя схемы.
Фрэйм як сцэнарый адносна працэсу навучання матэматыцы разглядаецца двух тыпаў. Да першага адносіцца фрэйм, які структуруе логіка-сэнсавыя адзінкі інфармацыі. Да другога – сцэнарны тып структуравання навучальнага матэрыялу. Пры такім падыходзе ад навучэнцаў патрабуецца не толькі размеркаваць матэрыял па слотах (паняцце, прымета, доказ і г.д.), але і ўсталяваць сэнсавыя і лагічныя сувязі паміж імі, аб’яднаўшы іх у адзіны фрэйм. Да другога тыпу адносіцца фрэйм-аповед – шкілетная форма выкладу досыць вялікага навучальнага матэрыялу ў выглядзе абагульненага плана, алгарытму дзеянняў, які можа выкарыстоўвацца шматразова.
Такім чынам, фрэймавы падыход дазваляе стварыць выяву-фрэйм матэматычнага матэрыялу ў знакава-сімвальнай сістэме. Тым самым перад навучэнцам устае праблема, якая патрабуе прадумвання і ўсведамлення кожнага афармляемага блока. Такая разумовая работа дазваляе сістэматызаваць веды (аналіз, сінтэз), замацаваць веды, вучыцца прымяняць веды, самаўдасканальвацца, самаразвівацца і развіваць творчыя і пазнавальныя здольнасці. Адпаведна, трансфармуючы наяўныя веды, навучэнец будзе развіваць пазнавальную самастойнасць у працэсе навучання матэматыцы.
Прыклады выкарыстання фрэймавага падыходу на ўроках матэматыкі
Пры вывучэнні ў 5-м класе прымет дзялімасці натуральных лікаў на 2, 3, 5, 9, 10 перад навучэнцамі можна паставіць задачу: самастойна пазнаёміцца з інфармацыяй падручніка па тэме, запоўніць прапанаваны фрэйм-каркас і размеркаваць прапанаваныя лікі па адпаведных прыметах.
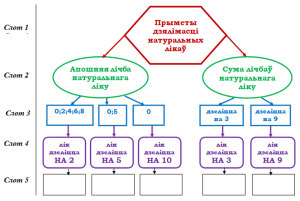
Аналагічныя фрэйм-каркасы можна выкарыстаць пры вывучэнні мностваў лікаў або лікавых прамежкаў у 8-м класе; формул каранёў квадратнага ўраўнення ў 9-м класе і г.д.
Пры вывучэнні ў 11-м класе формул плошчы бакавой паверхні і аб’ёму прызмы (цыліндра) можна выкарыстоўваць наступныя фрэймавыя схемы-апоры з запаўненнем пропускаў і пустых акенцаў у выглядзе  матэматычнымі тэрмінамі, формуламі, літарнымі абазначэннямі матэматычных велічынь і г.д.
матэматычнымі тэрмінамі, формуламі, літарнымі абазначэннямі матэматычных велічынь і г.д.
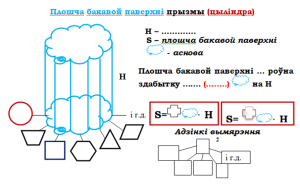
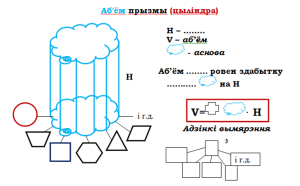
Аналагічныя фрэймавыя схемы-апоры можна выкарыстаць пры вывучэнні формул плошчы бакавой паверхні і аб’ёму піраміды (конуса).
Пры вывучэнні трыганаметрычных формул у 10-м класе наступны фрэйм-каркас паступова напаўняецца канкрэтным зместам:
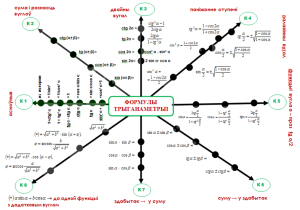
Аналагічным падыходам можна карыстацца пры вывучэнні трыганаметрычных функцый і іх уласцівасцей, вытворнай і яе прымяненняў і г.д.
Веды ў структураваным выглядзе “захоўваюцца” ў фрэйме, а настаўнік дапамагае навучэнцам арыентавацца ў састаўленай канструкцыі.
У параўнанні з традыцыйным урокам выкарыстанне фрэймавага падыходу дае магчымасць навучэнцам стаць актыўнымі ўдзельнікамі пазнаваўчага працэсу, што стымулюе іх да самастойнага пошуку, аналізу і сінтэзу інфармацыі, развівае іх пазнаваўчую зацікаўленасць да вывучэння прадмета матэматыкі.
З мэтай эфектыўнага засваення новага навучальнага матэрыялу і арганізацыі самастойнай работы па прадухіленні прабелаў у матэматычнай падрыхтоўцы фрэймавы падыход можна выкарыстоўваць пры вывучэнні новага матэрыялу; пры замацаванні пройдзенага на ўроку; пры падрыхтоўцы дамашняга задання; пры арганізацыі работы ў групах, парах; пры выніковым паўтарэнні.
Выкарыстанне фрэймавага падыходу ў навучанні матэматыцы дае магчымасць настаўніку стварыць для навучэнцаў сітуацыю, якая дазваляе за кароткі час самастойна асвоіць навучальны матэрыял і паспяхова прымяняць атрыманыя веды ў практычнай дзейнасці, пераносіць іх у новую жыццёвую сітуацыю. У выніку вырашаецца пытанне аптымізацыі працэсу навучання шляхам адыходу ад простага прайгравання гатовых ведаў да ўключэння навучэнцаў у самастойную пазнавальную дзейнасць, што спрыяе не толькі засваенню сістэмы ведаў, уменняў і кампетэнцый, якія складаюць інструментальную аснову вучэбнай дзейнасці навучэнцаў, але і развіццю асобы, і, як вынік, павышэнню эфектыўнасці навучання матэматыцы.



 Предложить публикацию
Предложить публикацию