Серия уроков геометрии по изучению темы «Четырехугольники» в 8-м классе

Серия уроков была разработана в рамках проекта «Четыре!», который был ориентирован на проектную деятельность на уроках математики и реализовывался при изучении темы «Четырехугольники» в 8-м классе.

Анна ОРЛОВСКАЯ,
учитель математики
ГУО «Средняя школа № 3 г. Островца»,
Гродненская область

Эта серия уроков посвящена исследованию четырехугольников – геометрических фигур, состоящих из четырех вершин и четырех сторон. Четырехугольники делятся на выпуклые и невыпуклые, что открывает возможности для глубокого анализа их свойств и применения в различных областях. На учебных занятиях рассматриваются различные типы четырехугольников, их особенности, а также практическое применение в архитектуре и планировке. Также охватываются основы геометрической классификации, включая параллелограммы и прямоугольники, что позволяет учащимся лучше понять и визуализировать эти фигуры.

Серия состоит из четырех уроков геометрии в 8-м классе по темам: «Параллелограмм», «Прямоугольник», «Ромб» и «Квадрат».

Идея: создание паспорта геометрических фигур.

Цель: изучить свойства и классификацию четырехугольников, а также их применение в геометрии.

Проблема заключается в недостаточной визуализации и понимании свойств четырехугольников у школьников.

Актуальность исследования вызвана необходимостью более глубокого понимания геометрических основ, что способствует развитию пространственного мышления и навыков архитектурного проектирования.

Задачи:

1. Изучить основные виды четырехугольников.

2. Исследовать геометрические свойства четырехугольников.

3. Рассмотреть применение четырехугольников в архитектуре и проектировании.

4. Разработать наглядные материалы для объяснения темы.

Параллелограмм. Конспект урока геометрии в 8-м классе

Цель: развитие функциональной грамотности при изучении темы «Параллелограмм».

Задачи урока

Образовательная: познакомить учащихся с геометрической фигурой параллелограмм, вырабатывать навыки решения геометрических задач. 

Развивающая: развивать умение применять методы математического моделирования (сравнение, классификация, анализ) при определении свойств и признаков параллелограмма; формировать умение выделять главное, анализировать и делать выводы; развивать устную речь, краткую письменную речь; развивать у учащихся умения работать в парах; развивать умение выполнять самооценку и взаимооценку; развивать трудолюбие, аккуратность, настойчивость в достижении цели.

Воспитательная: прививать культуру совместного умственного труда, уважительного отношения друг к другу; продолжить работу по реализации воспитательного потенциала, формированию у учащихся чувства патриотизма, гражданственности, уважения к созидательному труду как главному условию развития белорусского государства.

Методы обучения: репродуктивный, частично-поисковый, проблемный.

Формы организации познавательной деятельности: фронтальная, индивидуальная, парная.

Средства обучения: рабочая доска, интерактивная доска, мультимедийный проектор, ноутбук, раздаточный материал.

Структура урока:

I Организация начала урока.
II Постановка целей и задач.
III Актуализация знаний.
IV Объяснение нового материала.
V Динамическая пауза (историческая минутка).
VI Закрепление изученного материала.
VII Проектно-исследовательская деятельность (составление обучающимися дополнительных задач по предложенному плану).
VIII Обратная связь: рефлексия «Три М».
IX Домашнее задание.
X Итоги урока.

Ход урока

I Организация начала урока

– «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия». Эти слова, сказанные великим французским архитектором Ле Корбюзье в начале ХХ века очень точно характеризуют и наше время. Мир, в котором мы живем, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нем, открывать новое, понимать красоту и мудрость окружающего мира поможет вам эта наука.

– Добрый день, ребята! Я приглашаю вас в увлекательное путешествие в мир геометрии. Посмотрите на фигуры, размещенные на доске. Вы уже догадались, о чем сегодня пойдет речь? (Ответы учащихся: четырехугольники, геометрические фигуры.)

– Верно, мы отправимся в мир правильных и пропорциональных красивых фигур с помощью проекта «Четыре!».

II Постановка целей и задач

Притча «Основное правило достижения цели»

К Мастеру в стрельбе из лука пришли трое новичков:
– Ты самый ловкий стрелок во всём мире! Мы хотим стать такими же успешными и продолжить твоё дело, – сказали они.
– Я могу научить вас стрельбе из лука, рассказать все тайны и премудрости этого дела, – ответил Мастер. – Но в свои ученики я возьму только одного! И он сможет стать самыми лучшим стрелком и по-настоящему успешным человеком.
Чтобы выбрать кого-то к себе в ученики, Мастер предложил пройти всем троим небольшое испытание. Он повесил на дерево мишень, и на расстоянии нескольких метров подвёл первого новичка.
– Что ты видишь перед собой? – спросил Мастер.
– Я вижу дерево, на котором висит мишень.
– Что ещё? – спросил Мастер.
– Позади зелёная лужайка, на ней растут цветы.
– Хорошо, – сказал Мастер и подозвал следующего претендента в ученики.
– А ты что видишь перед собой?
– Я вижу мишень, дерево, поляну, цветы, небо, – ответил второй новичок.
– Хорошо! – ответил Мастер и задал такой же вопрос третьему новичку.
– А что видишь ты?
– Я вижу перед собой мишень! – ответил он.
– Хорошо, – сказал Мастер, – что ещё?
– Больше ничего! Самое главное – это мишень, я вижу только её!
– Молодец! – сказал Мастер. – Ты добьёшься в жизни больших успехов. Я возьму тебя в свои ученики.

– Когда есть цель, всё остальное не имеет значения.

Учитель предлагает ученикам поставить перед собой цель, с которой они пришли на урок, цель, которой они будут добиваться.

– Давайте попробуем сформулировать цель урока. Моя цель как учителя – рассмотреть свойства и признаки параллелограмма. А какую цель перед собой ставите вы? Можно ее записать в тетради. В конце урока вы для себя определите, достигли ли вы поставленной цели.

– Тема урока «Параллелограмм». (Записать на доске и в рабочих тетрадях)

III Актуализация знаний

1-й этап проекта. Тема и распределение ролей

– Давайте определим задачи нашего урока. Для начала вспомним что такое проект и как проходят наши уроки при создании проектов. (Ответы учащихся).

IV Объяснение нового материала

2-й этап проекта. Исследовательская работа

Задание. Сконструировать геометрическую фигуру – параллелограмм – из подручных средств (1-я группа – деревянные палочки и уголки, 2-я группа – пластмассовое трубочки, 3-я группа – металлическая проволока).

Заполнение паспорта параллелограмма совместно с учителем.

Практическая работа в парах (1 минута)

1. Противоположные стороны параллельны и равны.

– С помощью линейки измерьте противоположные стороны параллелограмма.

2. Диагонали точкой пересечения делятся пополам.

– С помощью линейки проверьте это свойство.  

Учащиеся делают вывод.

V Динамическая пауза (историческая минутка)

– Термин «параллелограмм» греческого происхождения и был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам. В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам. Он не рассматривает ни прямоугольника, ни ромба. Полная теория параллелограммов была разработана к концу средних веков и появились в учебниках лишь в XVII веке. Все теоремы о параллелограммах основываются непосредственно или косвенно на аксиоме параллельности Евклида.

Термин «диагональ» происходит от сочетания двух греческих слов «диа» (через) и «гониос» (угол), т. е. прямая, проходящая через вершины углов. Однако Евклид и большинство древнегреческих математиков пользовались почти всюду, в частности для прямоугольника, не этим, а другим термином – «диаметр». Это объясняется тем, что первые геометры мыслили о прямоугольнике, вписанном в круг. В средние века были в ходу оба термина. Фибоначчи и Региомонтан еще пользовались термином «диаметром». Лишь в XVIII веке термин «диагональ» входит в общее употребление.

VI Закрепление изученного материала. Решение задач

Работа в группах

Решение задач из учебника (№18 (а, б), № 19 (а, в), № 20, 24, 26, 29.

Группы по 6 человек. Каждой группе – по 3 задачи. Защита работы – анализ решения одной из задач.

VII Проектно-исследовательская деятельность

Составление обучающимися дополнительных задач по предложенному плану (дополнительный балл).

– Продолжая работу над проектом, предлагаю вам самим составить задачу (работа в парах).

Учащимися устно решается задание с комментированием всех используемых свойств прямоугольника.

VIII Обратная связь, итог урока

«Три М» (Три момента) 

Учитель попросит учащихся назвать три момента урока (темы), которые их больше всего удивили, заинтересовали или заставили поразмышлять.

Другим вариантом использования этого приема может стать просьба перечислить три самых трудных момента, с которыми справились.

IX Домашнее задание

Учебник: параграф 3, № 19(д), 28, 31.

X Итоги урока

Приложение

ПАСПОРТ ПАРАЛЛЕЛОГРАММА

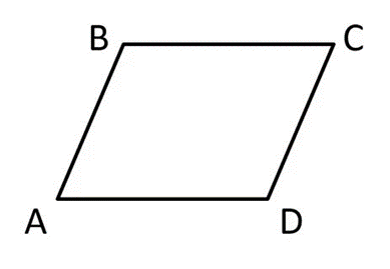Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

Прямоугольник. Конспект урока геометрии в 8-м классе

Цель: развитие функциональной грамотности при изучении темы «Прямоугольник».

Задачи урока

Образовательная: познакомить учеников с геометрической фигурой прямоугольник, вырабатывать навыки решения геометрических задач.

Развивающая: развивать умение применять методы математического моделирования (сравнение, классификация, анализ) при определении свойств и признаков прямоугольника; формировать умение выделять главное, анализировать и делать выводы; развивать устную речь, краткую письменную речь; развивать у учащихся умения работать в парах; развивать умение выполнять самооценку и взаимооценку; развивать трудолюбие, аккуратность, настойчивость в достижении цели.

Воспитательная: прививать культуру совместного умственного труда, уважительного отношения друг к другу; продолжить работу по реализации воспитательного потенциала, формированию у учащихся чувства патриотизма, гражданственности, уважения к созидательному труду как главному условию развития белорусского государства.

Методы обучения: репродуктивный, частично-поисковый, проблемный.

Формы организации познавательной деятельности: фронтальная, индивидуальная, парная.

Средства обучения: рабочая доска, интерактивная доска, мультимедийный проектор, ноутбук, раздаточный материал.

Структура урока:

I Организация начала урока.
II Постановка целей и задач.
III Актуализация знаний.
IV Объяснение нового материала.
V Решение практико-ориентированных задач.
VI Динамическая пауза.
VII Закрепление изученного материала.
VIII Проектно-исследовательская деятельность (составление обучающимися дополнительных задач по предложенному плану).
IX Обратная связь: рефлексия «Три М».
X Домашнее задание.
XI Итоги урока.

Ход урока

I Организация начала урока

– Добрый день! Ребята, я приглашаю вас в увлекательное путешествие в мир геометрии. Посмотрите на фигуры, размещенные на доске. Вы уже догадались, о чем сегодня пойдет речь? (Ответы учащихся: четырехугольники, геометрические фигуры.)

– Верно, мы продолжим работу с нашим проектом «Четыре!».

II Постановка целей и задач

Тема урока «Прямоугольник». (Запись на доске и в рабочих тетрадях).

– Начиная любое движение вперед, человек ставит перед собой цель, и нам в начале пути необходимо определить цель, к которой мы будем продвигаться на протяжении урока. Какова цель нашего урока?

Вместе с учителем учащиеся формулируют цель: рассмотреть свойства и признаки прямоугольника, доказать его особые свойства и признаки, формировать умения решать задачи с применением изученных свойств и признаков.

– Для достижения поставленной цели нам необходимо определить задачи. Что мы должны сделать, чтобы достичь намеченной цели? Составим план.

– Первое – изучить свойства прямоугольника, второе – научиться применять их при решении задач.

(Совместно с учащимися составить план урока: 1) изучить свойства прямоугольника; 2) научиться применять их при решении задач. Фиксируем на доске и в рабочих листах).

III Актуализация знаний

1-й этап проекта. Задачи по готовым чертежам

Фронтальный опрос по теме урока в форме игры «Паспорт».

1. Название / определение.
2. Свойства.
3. Признаки.

IV Объяснение нового материала

2-й этап проекта. Исследовательская работа

– Обратимся к математическим моделям, сконструированными вами. Прошу вас закрепить прочно все детали, чтобы получился параллелограмм. Из какой фигуры мы получили прямоугольник? (Ответы учащихся: из параллелограмма.)

– Какой вывод мы можем сделать? (Вывод учащихся: прямоугольник – это параллелограмм, у которого углы прямые.)

– Каким образом вы можете проверить, что данные модели – прямоугольники? (Ответы учащихся: используя транспортир, угол парты, угол учебника, тетради и т.д.)

– Таким образом, прямоугольник – это… у которого углы… (учащиеся заканчивают предложение).

– Продолжаем путь к поставленной цели! Перечислите свойства параллелограмма. (Ответы учащихся).

– Какие свойства должны быть присущи параллелограмму, чтобы он являлся прямоугольником? (Ответы учащихся).

– Верно, все свойства параллелограмма относятся к прямоугольнику. Проверьте справедливость свойств параллелограмма для прямоугольника.

Практическая работа в парах (1 минута)

1. Противоположные стороны параллельны и равны.

– С помощью линейки измерьте противоположные стороны прямоугольника.

2. Диагонали точкой пересечения делятся пополам.

– Приложите диагонали (модели диагоналей из картона) к прямоугольнику. Подтверждается свойство деления пополам точкой пересечения? Что вы можете сказать про длины диагоналей?

Учащиеся делают вывод.

V Динамическая пауза (физкультминутка)

VI Проектно-исследовательская деятельность

Составление обучающимися дополнительных задач по предложенному плану (дополнительный балл).

– Продолжая работу над проектом, предлагаю решить устно задачу.

Учащиеся устно решают задание с комментированием всех используемых свойств прямоугольника.

– Далее, какими свойствами должен обладать выпуклый четырехугольник, чтобы он являлся прямоугольником? (Ответы учащихся: перечисление рассмотренных свойств прямоугольника.)

– У нас нет линейки и транспортира, а нам необходимо доказать, что данный четырехугольник – прямоугольник. Есть только веревка и неровный лист бумаги. Докажите, что предлагаемая мною фигура – прямоугольник.

Проверка учащимися свойств прямоугольника практическим путем: с помощью веревки (прикладывая к одной стороне, затем к другой, замечая равные длины противоположных сторон, проверяя таким же образом равенство диагоналей) и с помощью неровного листа бумаги (сложив его пополам, затем еще раз пополам, получив прямой угол).

– Делая этот шаг, мы рассмотрели с помощью привычных предметов основные признаки прямоугольника.

Самостоятельная работа с проверкой по эталону

– Мы продолжаем составлять наш проект.

Задание № 1 (базовый уровень). 

– Вычислите периметр прямоугольника, если АВ = 12 см, ВС на 5 см длиннее стороны АВ.

Задание № 2 (повышенный уровень).

– В прямоугольнике ABCD диагонали пересекаются в точке О. Диагональ АС равна 10 см. Периметр треугольника АОВ 16 см, периметр треугольника ВОС 18 см. Найдите стороны прямоугольника и его периметр.

Задание № 3 (высокий уровень).

– Вычислите периметр прямоугольника АВСD, если биссектриса угла В пересекает сторону АD в точке Е и делит ее на отрезки АЕ = 17 см и ЕD = 21 см.

Включение в систему знаний и повторения

Задача. В параллелограмме АВСD диагонали равны. Угол САD равен 30⁰. Сторона СD равна 6 см. Найдите диагональ АС.

(Ученик решает у доски, оформляя условие, чертеж, комментируя решение, остальные учащиеся решают на рабочих листах.)

– И я предлагаю вам решить одну геометрическую задачу четырьмя способами решений. Вы работаете в группах. В течение 5 секунд определитесь с лидером группы, который возьмет на себя ответственность за работу группы. Каждой группе необходимо решить задачу на нахождение площади фигуры.

– Как вычислить площадь прямоугольника? (Ответ учащихся.)

1. На рабочем листе 1-й группы пунктиром дорисована фигура до прямоугольника, составлен план, что вычислять.

2. На рабочем листе 2-й группы пунктиром отрезаны прямоугольники, составлен план, что вычислять.

3. На рабочем листе 3-й группы пунктиром дорисована снизу фигура до прямоугольника, отрезаны боковые, составлен план, что вычислять.

4. На рабочем листе 4-й группы пунктиром дорисована фигура сбоку до прямоугольника, снизу отрезана часть, составлен план, что вычислять.

Все задачи оформлены на листе, разрезанном на четыре части. Каждый ученик решает свою задачу, затем, используя полученные ответы, совместно вычисляют площадь фигуры. Результат вычисления одинаковый у всех групп.

Проверяем результат, а так как он у всех должен получиться одинаковым, то все переворачивают карточку, на обороте карточки каждой группы нарисована следующая шахматная фигура и дан ключ. Оценка участников лидером группы.

VII Обратная связь, итог урока: подсчёт баллов, перевод в оценку, самооценка

«Три М» (Три момента) 

Попросите учеников назвать три момента урока/темы, которые их больше всего удивили, заинтересовали или заставили поразмышлять. Другим вариантом использования этого приема может стать просьба перечислить три самых трудных момента, с которыми справились.

VIII Домашнее задание

Учебник: параграф 4, № 54, 58, 68.

IX Итоги урока

Приложение

ПАСПОРТ ПРЯМОУГОЛЬНИКА

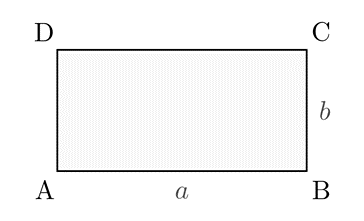Прямоугольник – это параллелограмм, у которого все углы прямые.

Ромб. Конспект урока геометрии в 8-м классе

Цель: развитие функциональной грамотности при изучении темы «Ромб».

Задачи урока

Образовательная: познакомить учащихся с геометрической фигурой ромб, вырабатывать навыки решения геометрических задач. 

Развивающая: развивать умение применять методы математического моделирования (сравнение, классификация, анализ) при определении свойств и признаков параллелограмма; формировать умение выделять главное, анализировать и делать выводы; развивать устную речь, краткую письменную речь; развивать у учащихся умения работать в парах; развивать умение выполнять самооценку и взаимооценку; развивать трудолюбие, аккуратность, настойчивость в достижении цели.

Воспитательная: прививать культуру совместного умственного труда, уважительного отношения друг к другу; продолжить работу по реализации воспитательного потенциала, формированию у учащихся чувства патриотизма, гражданственности, уважения к созидательному труду как главному условию развития белорусского государства.

Методы обучения: репродуктивный, частично-поисковый, проблемный.

Формы организации познавательной деятельности: фронтальная, индивидуальная, парная.

Средства обучения: рабочая доска, интерактивная доска, мультимедийный проектор, ноутбук, раздаточный материал.

Структура урока:

I Организация начала урока.
II Постановка целей и задач.
III Актуализация знаний.
IV Объяснение нового материала.
V Динамическая пауза.
VI Закрепление изученного материала.
VII Проектно-исследовательская деятельность (составление обучающимися дополнительных задач по предложенному плану).
VIII Обратная связь: рефлексия «Три М».
IX Домашнее задание.
X Итоги урока.

Ход урока

I Организация начала урока

– Добрый день! Я приглашаю вас в увлекательное путешествие в мир геометрии. Посмотрите на фигуры, размещенные на доске. Вы уже догадались, о чем сегодня пойдет речь? (Ответы учащихся: четырехугольники, геометрические фигуры.)

– Верно, мы продолжим работу с нашим проектом «Четыре!».

II Постановка целей и задач

– Тема урока «Ромб». (Записать на доске и в рабочих тетрадях).

– Начиная любое движение вперед, человек ставит перед собой цель, и нам в начале пути необходимо определить цель, к которой мы будем продвигаться на протяжении урока. Какова цель нашего урока?

(Вместе с учителем учащиеся формулируют цель: рассмотреть свойства и признаки ромба, доказать его особые свойства и признаки, формировать умения решать задачи с применением изученных свойств и признаков).

– Для достижения поставленной цели нам необходимо определить задачи. Что мы должны сделать, чтобы достичь намеченной цели? Составим план.

– Первое – изучить свойства ромба, второе – научиться применять их при решении задач. Главная задача – сопоставить свойства и признаки ромба с уже знакомыми геометрическими фигурами – параллелограммом и прямоугольником.

(Совместно с учащимися составить план урока: 1) изучить свойства ромба; 2) научиться применять их при решении задач. Фиксируем на доске и в рабочих листах).

III Актуализация знаний

1-й этап проекта. Задачи по готовым чертежам

	Найти угол АВК.
	ВС=5см. Найти периметр четырехугольника BDFM.
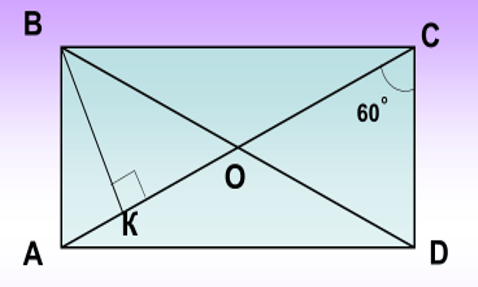	ОК=2см. Найти АС, АВ.

IV Объяснение нового материала

2-й этап проекта. Исследовательская работа

Сконструировать геометрическую фигуру – ромб – из подручных средств (1-я группа – деревянные палочки и уголки, 2-я группа – пластмассовые трубочки, 3-я группа – металлическая проволока).

Совместно с учителем учащиеся заполняют паспорт ромба.

Практическая работа в парах (вывод свойств и признаков ромба)

1. Противоположные стороны параллельны и равны.

– С помощью линейки измерьте противоположные стороны ромба.

2. Диагонали взаимно перпендикулярны и точкой пересечения делятся пополам.

– С помощью линейки и транспортира проверить эти свойства.  

(Вывод учащихся).

V Динамическая пауза (физкультминутка)

VI Закрепление изученного материала. Решение задач

Работа в группах

Решение задач из учебника (№ 71, 72, 74, 76, 26, 29)

Группы по 6 человек. Каждой группе по 3 задачи. Защита своей работы – анализ решения одной из задач.

VII Проектно-исследовательская деятельность

Составление обучающимися дополнительных задач по предложенному плану (дополнительный балл).

– Продолжая работу над проектом, предлагаю вам самим составить задачу (работа в парах).

Учащиеся устно выполняют задания с комментированием всех используемых свойств прямоугольника.

Самостоятельная работа

1. В ромбе АВСD диагонали пересекаются в точке О, <А = 31°. Найдите углы треугольника ВОС. (3-й уровень).

2. В прямоугольнике АВСD О– точка пересечения диагоналей, ВН и DЕ– высоты треугольников АВО и СОD соответственно, <ВОН = 60°, АН = 5см. Найдите ОЕ. (4-й уровень).

3. В ромбе АВСD угол В тупой. На стороне АD взята точка К, ВК перпендикулярно АD. Прямые ВК и АС пересекаются в точке О, АС = 2ВК. Найдите угол АОВ. (5-й уровень).

VIII Обратная связь, итог урока

«Три М» (Три момента) 

Попросите учеников назвать три момента урока/темы, которые их больше всего удивили, заинтересовали или заставили поразмышлять. Другим вариантом использования этого приема может стать просьба перечислить три самых трудных момента, с которыми справились.

IX Домашнее задание

Учебник: параграф 5, № 73, 77, 81.

X Итоги урока

Приложение

ПАСПОРТ РОМБА

Ромб – это параллелограмм, у которого все стороны равны.

Квадрат. Конспект урока геометрии в 8-м классе

Цель: развитие функциональной грамотности при изучении темы «Квадрат».

Задачи урока

Образовательная: познакомить учащихся с геометрической фигурой квадрат, вырабатывать навыки решения геометрических задач. 

Развивающая: развивать умение применять методы математического моделирования (сравнение, классификация, анализ) при определении свойств и признаков параллелограмма; формировать умение выделять главное, анализировать и делать выводы; развивать устную речь, краткую письменную речь; развивать у учащихся умения работать в парах; развивать умение выполнять самооценку и взаимооценку; развивать трудолюбие, аккуратность, настойчивость в достижении цели.

Воспитательная: прививать культуру совместного умственного труда, уважительного отношения друг к другу; продолжить работу по реализации воспитательного потенциала, формированию у учащихся чувства патриотизма, гражданственности, уважения к созидательному труду как главному условию развития белорусского государства.

Методы обучения: репродуктивный, частично-поисковый, проблемный.

Формы организации познавательной деятельности: фронтальная, индивидуальная, парная.

Средства обучения: рабочая доска, интерактивная доска, мультимедийный проектор, ноутбук, раздаточный материал.

Структура урока:

I Организация начала урока.
II Постановка целей и задач.
III Актуализация знаний.
IV Объяснение нового материала.
V Динамическая пауза
VI Закрепление изученного материала.
VII Проектно-исследовательская деятельность (составление обучающимися дополнительных задач по предложенному плану).
VIII Обратная связь: рефлексия «Три М».
IX Домашнее задание.
X Итоги урока.

Ход урока

I Организация начала урока

– Добрый день! Я приглашаю вас в увлекательное путешествие в мир геометрии. Посмотрите на фигуры, размещенные на доске. Вы уже догадались, о чем сегодня пойдет речь? (Ответы учащихся: четырехугольники, геометрические фигуры.)

– Верно, мы продолжим работу с нашим проектом «Четыре!».

II Постановка целей и задач

– Тема урока «Квадрат». (Записать на доске и в рабочих тетрадях).

– Начиная любое движение вперед, человек ставит перед собой цель, и нам в начале пути необходимо определить цель, к которой мы будем продвигаться на протяжении урока. Какова цель нашего урока?

(Вместе с учителем учащиеся формулируют цель: рассмотреть свойства и признаки квадрата, доказать его особые свойства и признаки, формировать умения решать задачи с применением изученных свойств и признаков).

– Для достижения поставленной цели нам необходимо определить задачи. Что мы должны сделать, чтобы достичь намеченной цели? Составим план.

– Первое – изучить свойства квадрата, второе – научиться применять их при решении задач. Главная задача – сопоставить свойства и признаки квадрата с уже знакомыми геометрическими фигурами – параллелограммом, прямоугольником и ромбом.

(Совместно с учащимися составить план урока: 1) изучить свойства квадрата; 2) научиться применять их при решении задач. Фиксируем на доске и в рабочих листах).

III Актуализация знаний

1-й этап проекта. Тема и распределение ролей

– Давайте определим задачи нашего урока. Для начала вспомним, что такое проект и как проходят наши уроки при создании проектов. (Ответы учащихся).

IV Объяснение нового материала

2-й этап проекта. Исследовательская работа

Сконструировать геометрическую фигуру – квадрат – из подручных средств (1-я группа – деревянные палочки и уголки, 2-я группа – пластмассовое трубочки, 3-я группа – металлическая проволока).

Совместно с учителем заполнение паспорта квадрата.

Практическая работа в парах (1 минута)

Противоположные стороны параллельны и равны.

– С помощью линейки измерьте противоположные стороны параллелограмма.

Диагонали точкой пересечения делятся пополам.

– С помощью линейки проверить это свойство.  

(Вывод учащихся.)

– Заполните таблицу, поставив знаки «+» (да) и «–»(нет).

Проверка результатов

V Динамическая пауза (физкультминутка)

VI Закрепление изученного материала. Решение задач

Работа в группах. Решение задач из учебника (№ 82, 83, 85, 87, 89, 90)

Группы по 6 человек. Каждой группе по 3 задачи. Защита своей работы – анализ решения одной из задач.

VII Проектно-исследовательская деятельность

Составление обучающимися дополнительных задач по предложенному плану (дополнительный балл).

– Продолжая работу над проектом, предлагаю вам самим составить задачу (работа в парах).

VIII Обратная связь, итог урока

«Три М» (Три момента). 

Попросите учеников назвать три момента урока/темы, которые их больше всего удивили, заинтересовали или заставили поразмышлять. Другим вариантом использования этого приема может стать просьба перечислить три самых трудных момента, с которыми справились.

IX Домашнее задание

Учебник: параграф 6, № 84, 88, 94.

X Итоги урока

Приложение

ПАСПОРТ КВАДРАТА

Квадрат – это прямоугольник, у которого все стороны равны.

Поделиться ссылкой: