Адна з мэт урока – фарміраваць уменні і навыкі выкарыстання формул вылічэння плошчы бакавой і поўнай паверхні конуса, рашэння практыка-арыентаваных задач.
Таццяна КЛАЧКОВА,
настаўнік матэматыкі
ДУА “Субацкая сярэдняя школа”
Ваўкавыскага раёна,
Гродзенская вобласць
Мэты:
– фарміраваць уменні і навыкі выкарыстання формул вылічэння плошчы бакавой і поўнай паверхні конуса, рашэння практыка-арыентаваных задач;
– забяспечыць умовы развіцця ўменняў граматна і дакладна выражаць свае думкі, аналізаваць і рабіць высновы, устанаўліваць прычынна-выніковыя сувязі, развіцця назіральнасці;
– садзейнічаць выхаванню настойлівасці, адказнасці, акуратнасці пры выкананні малюнкаў і запісу рашэння задач.
Задачы:
– ствараць умовы для фарміравання матэматычнай кампетэнцыі праз неабходнасць выкарыстання разнастайных прыёмаў і метадаў у працэсе работы з матэрыяламі ўрока;
– ствараць умовы для фарміравання вучэбна-пазнавальнай кампетэнцыі праз выкананне паслядоўных дзеянняў для дасягнення мэты;
– ствараць умовы для фарміравання каштоўнаснай кампетэнцыі праз абмеркаванне неабходнасці прымянення матэматычных ведаў для знаходжання выхаду з жыццёвых праблемных сітуацый.
Тып урока: урок адпрацоўкі ўменняў і навыкаў.
Метады: наглядныя, славесныя, умоўна-сімвалічныя, даследчыя.
Ход урока
I Арганізацыйна-матывацыйны этап
Дыдактычная задача: падрыхтоўка навучэнцаў да работы на ўроку.
Рэфлексіўная дзейнасць навучэнцаў: самаправерка.
Дзейнасць настаўніка па забеспячэнні рэфлексіі: праверка гатоўнасці.
Метады: славесныя.
Арганізацыйная форма: калектыўная.
II Пастаноўка мэты і задач урока
Дыдактычная задача: забяспечыць пастаноўку мэты і задач урока.
Рэфлексіўная дзейнасць навучэнцаў: пастаноўка мэты вучэбнай дзейнасці.
Дзейнасць настаўніка па забеспячэнні рэфлексіі: пастаноўка мэты і задач.
Метады: славесныя.
Арганізацыйная форма: калектыўная.
– Паглядзіце ўважліва на малюнак. Ён адпавядае тэме ўрока. Сфармулюйце тэму ўрока. Падказка: што можна вызначыць у конуса?

– Якія аб’екты маюць форму конуса?
– Дзе ў нашым жыцці яшчэ можна сустрэць конус?
– Такім чынам, тэма нашага ўрока – “Конус. Плошча поўнай і бакавой паверхні конуса. Аб’ём конуса. Рашэнне практыка-арыентаваных задач”. Запішам тэму ўрока.
– Якія задачы вы паставіце перад сабой?
– Эпіграфам да нашага ўрока стануць словы Бернарда Шоу: “Адзіны шлях, які вядзе да ведаў – дзейнасць”.
III Праверка дамашняга задання
Дыдактычная задача: забяспечыць праверку дамашняга задання.
Рэфлексіўная дзейнасць навучэнцаў: самаправерка, узаемаправерка.
Дзейнасць настаўніка па забеспячэнні рэфлексіі: арганізацыя праверкі дамашняга задання.
Метады: практычныя.
Арганізацыйная форма: індывідуальная.
1. Нямы дыктант
Настаўнік паказвае на малюнку элементы конуса. Вучні запісваюць іх назвы. Пасля выканання работы ажыццяўляецца самаправерка. Вучні правяраюць правільнасць выканання задання, падлічваюць колькасць правільных адказаў.
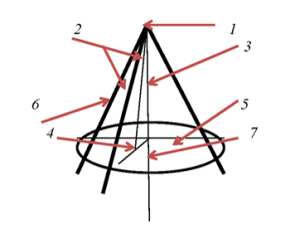
Адказы: вяршыня, утваральныя, вышыня, радыус, аснова, бакавая паверхня, вось.
2. Тэст
Тэст складаецца з 10 пытанняў. Вучні знаходзяць правільныя адказы і запісваюць нумары адказаў у радок. Ажыццяўляецца ўзаемаправерка.
Код: 1442331412. Сшыткі двух вучняў правярае настаўнік.
Тэст
|
1. Азначэнне конуса: |
1) Цела, абмежаванае паверхняй і кругамі. |
|
2. Што ўяўляе сабой бакавая паверхня конуса? |
1) Авал. |
|
3. Што ўяўляе сабой восевае сячэнне конуса? |
1) Авал. |
|
4. Што ўяўляе сабой сячэнне конуса плоскасцю, паралельнай аснове? |
1) Авал. |
|
5. Плошча асновы конуса: |
1) S = 2 πr2 |
|
6. Плошча бакавой паверхні конуса: |
1) S = 2 πr2 |
|
7. Вярчэннем якой геаметрычнай фігуры можна атрымаць конус? |
1) Вярчэннем прамавугольнага трохвугольніка вакол катэта. |
|
8. Колькі ўтваральных можна правесці ў конусе? |
1) Адну. |
|
9. Аб’ём конуса: |
|
|
10. Як зменіцца аб’ём конуса, калі радыус асновы павялічыць у 3 разы, а вышыню паменшыць у 5 разоў |
|
IV Актуалізацыя ведаў навучэнцаў
Дыдактычная задача: забяспечыць падрыхтоўку навучэнцаў да работы на ўроку.
Рэфлексіўная дзейнасць навучэнцаў: выкананне вусных практыкаванняў.
Дзейнасць настаўніка па забеспячэнні рэфлексіі: арганізацыя вуснай работы на ўроку.
Метады: славесныя, наглядныя.
Арганізацыйная форма: калектыўная.
– Ні адно рашэнне задач не абходзіцца без формул, адлюстроўваючых залежнасць паміж велічынямі.
1. “Узнаві формулу”
Дадзены пачатак формулы, трэба знайсці працяг формулы.
V = Sпоўн =
Sасн = с2 =
Sбак = С =
![]()
2. «Ланцужок задач»

V Фізкультмінутка
VI Трэніровачна-карэкцыйны этап
Дыдактычная задача: забяспечыць работу па рашэнні задач.
Рэфлексіўная дзейнасць навучэнцаў: рашэнне задач.
Дзейнасць настаўніка па забеспячэнні рэфлексіі: арганізаваць работу па рашэнні задач.
Метады: практычныя.
Арганізацыйная форма: калектыўная, індывідуальная.
Задача № 1
Ліхтар устаноўлены на вышыні 8 м. Вугал рассейвання святла 120°. Вылічыце, якую паверхню асвятляе ліхтар. (192 πм2)
Задача № 2
Адлегласць ад вяршыні ўзгорка да асновы – 200 м. Даўжыня асновы – 628 м. Знайдзіце вышыню ўзгорка і круцізну яго склона. (100√3 м, 60°)
Задача № 3 (самастойна)
Вылічыце вышыню маланкаадвода, калі радыус “абароненага” круга 15 м, а вугал паміж маланкаадводам і ўтваральнай конуса бяспекі 60°. (5√3 м)
VII Падвядзенне вынікаў урока
– Якія задачы вы ставілі перад сабой?
– Якое прасторавае цела называецца конусам?
– Як знайсці плошчу бакавой паверхні, поўнай паверхні?
– Як знайсці аб’ём конуса?
– Як вы ацэніце сваю работу на ўроку? Ці дасягнулі вы жаданых вынікаў?
– Над чым яшчэ трэба папрацаваць?
VIII Дамашняе заданне
§ 3, № 464, № 466.



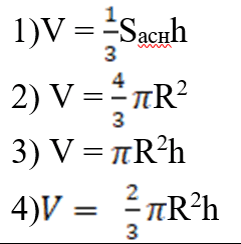


 Предложить публикацию
Предложить публикацию