Татьяна КНЫШ,
учитель математики
гимназии № 1 им. Ф.Я.Перца Пинска
Цель: повышение профессиональной компетентности педагогов по изучению раздела “Тригонометрия” путём использования приёмов мнемотехники.
Задачи:
- создать условия для позитивного настроя и мотивационной готовности участников к совместной работе над темой;
- организовать взаимодействие участников по освоению и отработке приёмов мнемотехники;
- стимулировать творческую деятельность участников по применению умений, приобретённых в ходе мастер-класса в своей дальнейшей практической деятельности.
Уважаемые коллеги, добрый день! Приятно видеть вас в этой аудитории, очень надеюсь, что время, отведенное для нашего общения, будет приятным и полезным.
Для начала давайте с вами познакомимся. На столах у вас есть бумажки оранжевого цвета. Напишите, пожалуйста, на них каждый своё имя и одну наиболее важную черту своего характера. Например: я – Татьяна, добрая. Спасибо.
Наш мастер-класс мне бы хотелось начать с притчи. В Греции на острове Хеосс до нашей эры случилось землетрясение, засыпавшее дом богача и гостей, пировавших с хозяином в его большом доме. Когда людей раскопали, по их останкам было трудно определить, кто, где лежит. Единственный оставшийся в живых человек, учитель риторики и поэт Симонид, незадолго до трагедии вышедший из дома, легко вспомнил, кто, где сидел и кто что делал. Так родственники опознали тела своих близких, а Симонид стал основоположником нового метода запоминания (Как вы думаете какого метода?) – топологической мнемоники, согласно которой для запоминания большого количества материала достаточно расположить его в знакомом пространстве (например, собственной квартире) и по мере надобности «доставать» (находить) его.
Учение Симонида состояло из двух важных понятий – ассоциация и фон.
– Уважаемые коллеги, пожалуйста, дайте определение этим двум понятиям.
Ассоциация – мысленная связь между двумя предметами, фон – это то, что вы хорошо знаете до мельчайших подробностей. Тогда, для того чтобы запомнить множество каких-то фактов, их нужно соединить (ассоциировать) с тем, что вам хорошо знакомо.
Симонидовский метод широко использовал Цицерон, который проговаривал свою речь, шагая из комнаты в комнату. Выступая перед публикой, он проходил мысленно тот же путь, собирая «разбросанные» по пути факты и изречения.
– Дайте, пожалуйста, определение «мнемонике».
Мнемоника – искусство запоминания.
– А с помощью чего мы запоминаем ту или иную информацию? (приёмы и способы различные применяем). Правильно!
Совокупность специальных приёмов и способов, облегчающих запоминание нужной информации, называется мнемотехникой.
Философ и поэт Джордано Бруно преподавал мнемотехнику. Ею интересовались Аристотель, Александр Македонский. Феноменальной памятью обладали Юлий Цезарь и Наполеон Бонапарт. Впоследствии мнемоника на долгие годы была забыта.
Однако возросшее количество информации и необходимость запоминать много и надолго возродило интерес к этой области практической психологии.
Самое грандиозное поле деятельности для применения мнемотехники– это школа.
– Уважаемые коллеги, как вы думаете почему?(большое количество правил, которые ребенку нужно запомнить на уроках). Правильно! Большое количество правил, ребята учат на уроках русского и белорусского языка и математики. Эти предметы в школе считаются самыми трудными, и по ним учащиеся 9-х и 11-х классов сдают экзамен. Я как учитель математики заинтересована в том, чтобы мои дети сдали экзамен на «хорошо» и «отлично».
Я предлагаю вам написать на стикере, что вы ожидаете от этого занятия. Приклейте, пожалуйста, свой стикер на доску.
(на экране тема, цель и задачи мастер-класса)
– Приведите примеры мнемотехник, которые используются на уроках математики.
Пример №1. БИССЕКТРИСА – это крыса, которая бегает по углам и делит угол пополам.
Пример № 2. МЕДИАНА – обезьяна, лазаетпо сторонами делит их пополам.
Пример № 3. Правильную дробь сравнивают со снеговиком, у которого голова меньше туловища (голова – числитель, туловище – знаменатель). Неправильная дробь – голова у снеговика больше туловища или равна ему.
На уроках математики таких примеров мнемотехники можно использовать большое количество. Ребята очень хорошо запоминают правило с чем-то его ассоциируя. Такие приемы часто используются в основном в начальной и средней школе с 5-го по 7-й класс в игровых формах. С 8-го класса учителя интенсивно начинают готовить детей к экзаменам и совсем забывают про такие формы работы на уроках. Но ведь в старших классах намного больше теории по математике, чем в начальной и средней школе, поэтому мнемотехнику нужно продолжать и у них, потому что опыт показывает, что большая часть старшеклассников с легкостью вспоминают мнемотехники, но гораздо тяжелее дело обстоит с припоминанием правил.
Мнемотехники позволяют экономить время на уроках повторения и систематизации пройденного, особую пользу они приносят при подготовке к экзамену и ЦТ. В 10–11-х классах на уроках математики уделяется большое внимание изучению такого раздела, как «Тригонометрия». Этот раздел сложен тем, что в нем большое количество тригонометрических формул, которые ребята не запоминают и задания, связанные с этим разделом, на экзаменах не выполняют правильно, либо вообще к ним не приступают.
Поэтому я сегодня предлагаю по-другому взглянуть на раздел «Тригонометрия».
– С чего начинается изучение раздела «Тригонометрия»? (с изучения тригонометрических функций (y=sinx, y=cosx, y=tgx и y=ctgx), знаков тригонометрических функций, значения тригонометрических функций некоторых углов, формул приведения, основное тригонометрическое тождество и т.д.) Правильно! Давайте более подробно рассмотрим поэтапно, каждую из этих тем с применением мнемотехники.
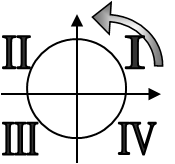
Введение понятия «единичная окружность» – «стадион». Окружность с центром в точке (0;0) – центр стадиона. Определяем начало – “старт”. Определим направление “бега” – против часовой стрелки, как на всех спортивных стадионах, аренах цирка.
Определяем сектора – “трибуны зрителей”(также против часовой стрелки). Таким образом, получили единичную окружность готовую для работы.
«Ось синусов, ось косинусов». При запоминании, какая из осей координат является осью синуса, а какая косинуса, можно воспользоваться следующим приемом:
При произношении слова «синус» акцентируем внимание на первой букве слова – СССинус. СССинус – СССверху
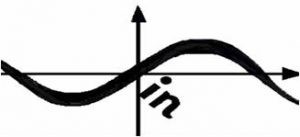
При рассмотрении всех свойств необходимо уметь “читать по графику”. Но сначала будем читать сами графики. Оказывается, имя графика можно «прочитать» через точку (0;0)
Аналогично рассматриваем график функции у = cos х и подписываем на координатной плоскости имя графика («читая» имя через точку (0,0)).
Тригонометрические функции разделите на врагов и друзей. Друзья – человечки Синус, Тангенс и Котангенс, их враг – Косинус. Почему именно так объединяю функции? Потому что между первыми тремя функциями много общего. Например, Синус, Тангенс и Котангенс нечетные, а Косинус четный.
Ввожу данное свойство на мнемоприеме «Сладкоежек», говорю, что первые три человечка конфетки не едят и как капризные детки их выплевывают, а вот Косинус их враг сладкоежка и конфету съедает.
При решении простейших тригонометрических уравнений первые три функции Синус, Тангенс, Котангенс имеют период , а их враг Косинус – период .
Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Ключевое слово – два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там – два. Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет 2πn. А ещё наоборот бывает. Пропустит человек знак ±, доберётся до конца, напишет правильно 2πn, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.
Значения тригонометрических функций некоторых углов (Уважаемые коллеги, я предлагаю вам по памяти восстановить таблицу значений тригонометрических функций углов равных 0°, 30°,45°,60°,90°). Хорошо!
У каждого человека более или менее развиты слуховая, зрительная, образная, моторная память, оперативная память. Я стараюсь подбирать опоры на «слух», «образ», «зрение».
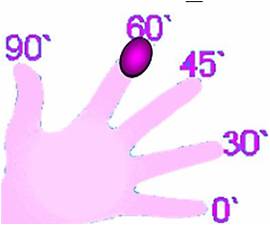
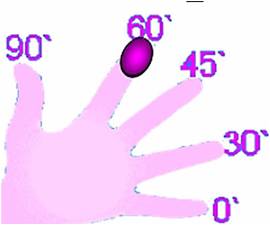
А теперь пример на развитие моторной и оперативной памяти. Одним из важных вопросов тригонометрии является знание значений «хороших» углов: 0°, 30°, 45°, 60°, 90°. И если «Математику надо знать как свои пять пальцев», то используем эти пальцы. Ни карандаш, ни бумага не нужны, а только левая ладонь.
Каждому пальцу соответствует «хороший» угол.
Мизинцу – 0°
Безымянному – 30°
Среднему – 45
Указательному –60°
Большому – 90°
Учащимся необходимо помнить только, что любая функция – это отношение.«До» – количество пальцев снизу, «после» – сверху.
Для вычисления синуса «хорошего» угла используем формулу:
Для вычисления косинуса и тангенса используем формулы:
Получаем таблицу значений тригонометрических функций для углов 30°, 45°,60° и 900.
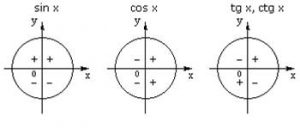
– Изобразите, пожалуйста, знаки тригонометрических функций на окружности). Спасибо!
Важно помнить, что:
- все тригонометрические функции в I четверти принимают положительные значения(знак «+»). (Проверили? Верно, поставили знак «+»в I четверти для каждой функции?);
- у синуса знаки расположены горизонтально,
- у косинуса – вертикально,
- у тангенса и котангенса – крест-накрест.
Знаки тригонометрических функций
Учащиеся прекрасно запоминают, что у тангенса и котангенса знаки располагаются крест-накрест, но забывают, у какой функции (синуса или косинуса), знаки расположены горизонтально, а у какой – вертикально. В этом случае поможет следующее правило: произносить слова «синус» и «косинус» нужно нараспев, выделяя ударную гласную и фиксируя при этом, в каком направлении вытягивается рот. При произнесении слова «синус» ударная гласная «и» вытягивает рот в направлении «↔», значит, у синуса знаки расположены горизонтально. Аналогично, при произнесении слова «косинус», ударная гласная «о» вытягивает рот в направлении «↕», значит, у косинуса знаки расположены вертикально.
При решении простейших тригонометрических уравненийsinx = a, cosx = a ученики забывают, какую хорду и в каком случае нужно рассматривать. Опять поможет произнесение слов «синус» и «косинус». Ударная гласная «и» вытягивает рот в направлении «↔», значит, на круге при решении уравнения sinx = a надо провести горизонтальную хорду, ударная «о» вытягивает рот в направлении «↕», значит, при решении уравнений вида cosx = a будем проводить вертикальную хорду.
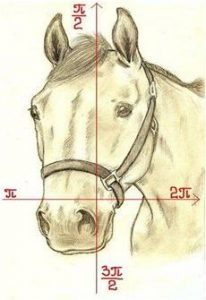
Формулы приведения (Лошадиное правило).
В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции (синус на косинус), смотрел на свою умную лошадь. Она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента
π/2 ± α (3π/2 ± α) или π ± α (2π ± α).
Если лошадь кивала головой вдоль оси ОУ (вертикального диаметра окружности), то математик считал, что получен ответ «да, менять», если вдоль оси ОХ (горизонтального диаметра окружности), то «нет, не менять».
Это правило действовало, только для смены синуса на косинус и наоборот. Оставалось, только определить знак функции – это зависело от того в какой четверти располагалась эта точка и знака тригонометрической функции в той или иной четверти.
Задание для группы учителей
Задание. Найти значение выражения
![]()
(Дается время группе для выполнения данного задания)
Решение: Сначала следует выполнить подготовительный момент: представить данное выражение в виде
Предположим, что мы выбрали первый из представленных видов. Тогда, применяя первое правило, получим, что в III четверти косинус отрицательный (ставим знак «минус»). Далее задаем вопрос лошади: «Меняем или не меняем функцию?». 180° попадают на горизонтальный диаметр. Помотав головой вдоль этого диаметра, получаем ответ: «Нет, не меняем». Получим
Теперь предположим, что мы выбрали второй из представленных видов. Вопрос со знаком решается аналогично – ставим знак «минус». А задавая вопрос: «Меняем или не меняем функцию?» и, помотав головой вдоль соответствующего диаметра, получаем ответ: «Да, меняем», так как 270° попадают на вертикальный диаметр. Получим![]()
Основное тригонометрическое тождество можно ребятам преподнести в виде стишка.
Косинус квадрат
очень рад:
К нему едет брат –
синус квадрат.
Когда встретятся они,
окружность удивится:
выйдет целая семья, то есть единица.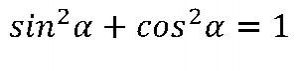
Формулы понижения степени.
Важно понять структуру этих формул, в частности, такой момент: «степень понижается, а угол становится в два раза больше». Эти формулы очень похожи друг на друга, поэтому для лучшего их запоминания следует применять правило: «Единица минус – дает синус, а единица плюс – дает косинус».
Слайд Запоминание формул сложения:![]()
![]()
![]()
![]() В этих формулах синус ведет себя «правильно» (если в левой части стоит знак «+», то и в правой «+», а если в одной части формулы « – », то и в другой части знак « – ») и «любит» косинус. А косинус ведет себя неправильно (если слева – плюс, то справа – минус и наоборот) и «любит» только самого себя.
В этих формулах синус ведет себя «правильно» (если в левой части стоит знак «+», то и в правой «+», а если в одной части формулы « – », то и в другой части знак « – ») и «любит» косинус. А косинус ведет себя неправильно (если слева – плюс, то справа – минус и наоборот) и «любит» только самого себя.
Подводя итоги опыта работы с применением мнемотехники, я сделала вывод, что лишь прикоснулась к большому источнику идей и открытий, позволяющих сделать обучение простым и доступным для каждого ученика. Именно творчество в работе, использование приемов и методов мнемотехники помогает моему самовыражению в профессии.
Уважаемые коллеги, в заключение я бы хотела услышать от вас, целесообразно ли использование мнемотехники при изучении тригонометрии.
Уважаемые коллеги, оправдались ли ваши ожидания от мастер-класса? Как вы считаете, пригодятся ли вам полученные навыки в дальнейшей педагогической деятельности?
Используя кубик, я предлагаю подвести итоги нашего с вами сотрудничества:
– На мастер-классе я…
– Самым интересным для меня сегодня было…
– В своей дальнейшей работе я…
– Я бы хотел пожелать, посоветовать…
– Самым неожиданным для меня было…
– Самым полезным …
Благодарю вас за работу, желаю вам вдохновения, творчества. Своё выступление на мастер-классе я хотела бы закончить словами К.Д.Ушинского: «Учите ребенка каким-нибудь неизвестным ему пяти словам, он будет долго и напрасно мучиться, но свяжите двадцать слов с картинками, и он усвоит их на лету».












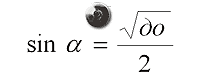






 Предложить публикацию
Предложить публикацию