Задачи на все действия с рациональными числами. Урок математики в 6-м классе

Светлана ЖУК,
учитель математики
ГУО «Гимназия №1 г. Мосты»,
Гродненская область

Цели:

— предполагается, что к окончанию урока учащиеся будут уметь применять правила сложения, вычитания, умножения и деления положительных и отрицательных чисел путём применения разнообразных форм упражнений (решение примеров, уравнений, упрощение выражений);
— создать условия для развития исследовательских способностей, вычислительных навыков, логического мышления, навыков само- и взаимоконтроля, способствовать развитию умения выделять главное, переносить знания в новую ситуацию, сотрудничать и работать в парах;
— содействовать формированию положительной мотивации и интереса к предмету; воспитанию культуры общения, бережного отношения к своему здоровью.

Формы организации учебной деятельности: индивидуальная, работа в паре, группе.

Ход урока

1 Организационно-мотивационный момент

– Здравствуйте, ребята. Рада всех видеть в хорошем настроении, присаживайтесь.

Тема нашего сегодняшнего урока «Задачи на все действия с рациональными числами». Откройте тетради, отступите четыре клетки от вашей последней записи, запишите число, классная работа и тему урока.

Предлагаю вам, используя «Облако слов», определить задачи на сегодняшний урок (учащиеся предлагают свои варианты).

– Правильно, сегодня на уроке мы закрепим умения и навыки сложения, вычитания, умножения и деления положительных и отрицательных чисел путём применения разнообразных форм упражнений (решения примеров, уравнений), что послужит вам хорошей основой при дальнейшем обучении.

Эпиграфом сегодняшнего урока я взяла слова швейцарского педагога, жившего в конце XVIII – начале XIX веков Песталоцци: «Счёт и вычитание – основа порядка в голове». Как вы понимаете данные слова?

Сегодня на уроке оценивать себя вы будете сами, у каждого на парте лист оценки, в котором указаны все этапы сегодняшнего урока и количество баллов, которые вы можете получить за него.

2 Проверка домашнего задания

– Начнем с проверки домашнего задания. Предлагаю посмотреть на слайд и сверить ответы (на слайде записано решение упражнений, в которых сделаны ошибки)

№ 280. Определить знак значения выражения, не выполняя вычисления:

а) выражение1 > 0 ;   выражение2 < 0.
б) выражение1 > 0 ;   выражение2 > 0.

№ 281. Найти среднее арифметическое чисел.

Все, кто выполнил оба задания правильно, поставят в лист самооценки 2 балла, кто одно – 1 балл, у кого ошибки в 1 и 2 задании – 0 баллов.

3 Актуализация опорных знаний

Продолжи предложение:

–  Множество целых чисел –  это…
–  Множество рациональных чисел –  это…
–  Противоположные числа –  это ….
–  Модуль числа –  это…
–  Из двух отрицательных чисел большим будет….
–  Сумма двух отрицательных чисел будет числом ….
–  Произведение двух отрицательных чисел будет числом ….
–  Частное двух чисел с разными знаками будет числом ….
–  Если количество отрицательных множителей чётно, то произведение будет …
– Если количество отрицательных множителей нечётно, то произведение будет …

За каждый правильно сделанный ответ – 1 балл. Количество баллов запишем в лист оценки.

«Верно – неверно»

К доске вызываются двое учащихся, остальные самостоятельно в тетради.

– Если согласны с моим утверждением, ставим «плюс», если не согласны ставим «минус». – 5 – отрицательное число (верно). 

1) Расстояние от начала отсчета до точки с координатой – 3, равно – 3 единицам (неверно).
2) 6 – положительное число (верно).
3) – 9 и 9 противоположные числа (верно).
4) Модуль – 7 равен – 7 (неверно).
5) 0 – положительное число (неверно).
6) Сумма двух отрицательных чисел является отрицательным числом (верно).
7) Произведение двух целых положительных чисел равно 0 (неверно).
8) Произведение двух отрицательных чисел является положительным числом (верно).
9) Сумма противоположных чисел равна 0 (верно).

Таблица ответов

– Обменяйтесь, пожалуйста, тетрадями, возьмите карандаши и проверьте работу своего одноклассника. Подсчитайте количество правильных ответов и поставьте на полях. Количество баллов запишем в лист оценки.

4 Практический этап

Викторина (работа за компьютером)

– Умение применять правила сложения, вычитания, умножения и деления предлагаю проверить при выполнении задания за компьютером.

https://learningapps.org/watch?v=pri7ahym321

Количество правильных ответов вносится в таблицу оценивания.

Физминутка

Работа в группах

– У каждой группы на парте лежат шестиугольники (гексы), на которых записаны уравнения. Из всех уравнений вы должны выбрать те, решение которых есть ключевое число и в соты.

Первая группа, ключевой шестиугольник число – 11;
вторая группа – число – 13;
третья группа – число – 15;
четвёртая группа – число – 16;
пятая группа – число – 18.

Представитель группы должен защитить работу.

Каждая правильно подобранная гекса – 1 балл. Максимум – 6 баллов. За активную работу в группе – плюс 2 балла.

Выступление учащегося

Долгое время люди отрицательные числа считали несуществующими, «ложными». Этим числам сопоставлялись различные понятия, чтобы удобнее было осмыслить результаты действия с ними. Например, индийские математики Брамагупта и Бхаскара связывали положительные и отрицательные числа с понятиями «долг», «имущество»

Правила умножения, деления, сложения и вычитания были предложены в III веке греческим математиком Диофантом. Они звучали примерно так: «вычитаемое, умноженное на прибавляемое, дает вычитаемое», «вычитаемое, умноженное на вычитаемое, дает прибавляемое»

В VII веке индийский математик Брамагупта правила сложения и вычитания отрицательных чисел выражал так: «Сумма двух имуществ есть имущество», «сумма двух долгов есть долг».

О знаке результата, получаемого при умножении двух отличных от нуля чисел, известно и такое правило древних:

1 «друг моего друга – мой друг» (+) (+) = (+)
2 друг моего врага – мой враг (+) (–) = (–)
3 враг моего друга – мой враг (–) (+) = (–)
4 враг моего врага – мой друг. (–) (–) = (+)

И так было до XVII века, математики все еще не признавали отрицательных чисел, называли их «меньшими, чем ничто». Лишь в XVII веке голландский математик Жирар стал пользоваться отрицательными числами наравне с положительными. Так появились рациональные числа, которые состоят из целых и дробных положительных чисел, им противоположных отрицательных и нуля.

5 Контрольно-коррекционный этап

Самостоятельная работа.

Необходимо восстановить цепочку вычислений.

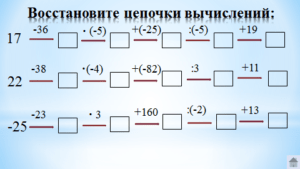
За каждую цепочку в лист оценки выставляем по 5 баллов.
Сделать анализ наиболее существенных ошибок и затруднений.

6 Подведение итогов урока

– А теперь, когда вопросы исчерпаны, давайте подведем итоги. Предлагаю подсчитать количество набранных баллов за урок и выставить себе отметку.

7 Рефлексия. Домашнее задание

– Знания, которые усваивает человек, открывают ему с дверь к другим, новым знаниям и достижениям. И в зависимости от того, какие это знания – трудные или легкие, интересные или не очень, можно дать определение и той двери, которая перед нами открывается, – тяжелая металлическая или наоборот, невесомая, легкая из картона.

Будем считать, что действия с отрицательными числами мы изучили. Трудно ли вам было, легко ли? Как для себя вы оцените эти знания, подберите наиболее соответствующее вашим ощущениям понятие и продолжите предложение:

— Я научился…
— Было трудно…
— Сегодня я узнал…
— У меня получилось…
— Теперь я могу…

Лист оценки

Таблица для выставления оценки

Поделиться ссылкой: