В материале затрагивается проблема развития информационной компетентности учащихся на уроках математики. Основное внимание направлено на рассмотрение информационной компетентности как интегративного качества личности. В статье приведены описания различных типов задач, способствующих формированию информационной компетентности учащихся, приводятся конкретные примеры на каждый тип задач.
Галина ГЛЯК,
учитель математики
ГУО «Средняя школа № 17 г. Орши»,
Витебская область
Эффективность деятельности человека напрямую зависит от способности оперативно находить необходимую информацию и использовать ее для решения своих проблем, поэтому в современных условиях особое внимание должно уделяться обучению учащихся работе с информацией. Интенсивные потоки накопления информации, быстрые темпы устаревания знаний в современном мире и ограниченные возможности их усвоения личностью – основное противоречие, которым обусловлена актуальность развития информационной компетентности учащихся.
В педагогической науке существует разногласие по определению понятия «информационная компетентность». Во-первых, данный термин можно понимать, как умение обращаться с компьютерной техникой и компьютерными средствами в информационных процессах. Во-вторых, информационную компетентность рассматривают как свойство личности, позволяющее человеку выполнять операции над информацией с помощью информационных технологий.
Мы будем рассматривать информационную компетентность как интегративное качество личности, являющееся результатом отражения процессов отбора, усвоения, переработки, трансформации и генерирования информации в особый тип предметно-специфических знаний, позволяющее вырабатывать, принимать, прогнозировать и реализовывать оптимальные решения в различных сферах деятельности как новую грамотность, в состав которой входят умения активной самостоятельной обработки информации человеком, принятие принципиально новых решений в непредвиденных и нестандартных ситуациях [5].
В научной литературе общепринята точка зрения, согласно которой понятие «компетентность» включает знания, умения, навыки, а также способы выполнения деятельности.
Деятельность учащихся на уроках математики реализуется через решение различных задач.
В основание типологии задач, предложенной коллективом авторов в учебном пособии «Компетентностно-ориентированные задания в системе высшего образования», положены умения работы с информацией, поскольку информационная компетентность является надпредметной, необходимой для решения любой задачи, входящей в состав различных общекультурных и профессиональных компетентностей[3].
Типы компетентностно-ориентированных задач, которые мы охарактеризуем в этой работе:
1) задача-интерпретация;
2) задача-сравнение;
3) задача-аналогия;
4) задача-модель;
5) задача – поиск прообраза;
6) задача-структурирование;
7) задача-возможность;
8) задача на избыточность;
9) задача на недостаточность.
1. Задача-интерпретация (текстовой, графической, символьной информации) ориентирована на использование приема интерпретации, т.е. на распознавание объекта изучения среди других объектов (раскрытие значений), либо на рассмотрение объекта в плане разных понятий (раскрытие смысла). В ходе решения такого типа задач, учащиеся приобретают опыт в обнаружении новых связей и отношений межу объектами.
Пример. Алгебра, 9-й класс. Тема «Системы нелинейных уравнений».
Определите количество решений системы уравнений
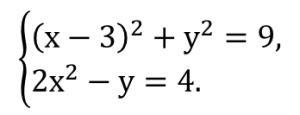
Одним из эффективных приёмов поиска решения данной задачи является геометрическая интерпретация функционально-графическим методом. Достаточно построить окружность с центром в точке (3; 0) и радиусом 3 и параболу , а затем определить количество точек пересечения графиков.
2. Задача-сравнение (качественного и количественного) предполагает использование приема сравнения – выделение сходных и различных свойств у рассматриваемых объектов.
Пример. Геометрия, 8-й класс. Тема «Четырехугольники».
При изучении темы учащимся предлагаются определения прямоугольника, ромба и квадрата, на основании которых требуется определить общие и частные свойства геометрических фигур.
Задание 1. На основании определений геометрических фигур установите их свойства.
Определения:
1) прямоугольником называется параллелограмм, у которого все углы прямые;
2) ромбом называется параллелограмм, у которого все стороны равны;
3) квадратом называется прямоугольник, у которого все стороны равны.
Примеры рассуждений:
– прямоугольник является параллелограммом, значит, обладает всеми свойствами параллелограмма (учащиеся перечисляют свойства параллелограмма);
– ромб является параллелограммом, значит, обладает всеми свойствами параллелограмма (учащиеся перечисляют свойства параллелограмма);
– квадрат является прямоугольником, а, следовательно, параллелограммом, значит, обладает всеми свойствами параллелограмма (учащиеся перечисляют свойства параллелограмма).
Задание 2. Изобразите данные геометрические фигуры. Проведите в каждой из них диагонали. С помощью рассуждений установите свойства диагоналей в каждой из фигур.
3. Задача-аналогия направлена на получение новой информации об объекте на основании установления сходства (аналогии) некоторого малоизученного объекта с хорошо известным объектом в форме гипотезы.
В книге «Математическое открытие» [4] Дж.Пойа пишет, что аналогия является обильным источником новых фактов. В простейших случаях можно почти копировать решение подобной задачи. Аналогия только указывает направление, в котором следует продолжать работу.
Опыт в умении проводить аналогию позволяет учащимся переносить уже имеющиеся знания в новую, измененную ситуацию, что позволяет облегчить процесс обучения.
Пример. Алгебра, 9-й класс. Тема «Сложение и вычитание рациональных дробей».
Учащимся предлагается выполнить следующее задание:
Используя метод аналогии, учащиеся с легкостью решат поставленную задачу.
4. Задача-модель (знаково-символическая, образная) подразумевает применение приема моделирования для дальнейшего получения информации об изучаемом объекте.
Пример. Математика, 5-й класс. Задача на совместную работу [2].
№ 202. Через один кран бак вместимостью 600 л можно наполнить за 10 мин, а через второй – за 15 мин. За сколько минут наполняется бак через оба крана?
По условию задачи учащимся предлагается составить таблицу данных.
Такие таблицы данных являются моделями решения задач. В ходе решения учащимся требуется представить текст задания при помощи математической символики в виде таблицы и заполнить ее недостающими данными.
| Объект | Вместимость бака, л | Время заполнения бака, мин |
Скорость заполнения бака, л/мин |
| 1-й кран | 600 | 10 | |
| 2-й кран | 600 | 15 | |
| Оба крана | 600 | ? |
При работе с таким типом задач необходимо понимать, что одного составления модели к задаче недостаточно. Следует предлагать учащимся и обратные задания, а именно: составление текстов задач по модели.
В процессе работы с таким типом задач учащиеся приобретают опыт построения моделей реальных явлений, исследования явления по заданным моделям.
5. Задача – поиск прообраза предполагает поиск реального объекта или явления, иллюстрирующего некоторое свойство или отношение с другими объектами. Задачи такого типа помогают учащимся понять, что математика это окружающий нас мир, который просто описан с помощью другого языка.
Пример. Математика, 6-й класс. Тема «Наглядные представления тел в пространстве, примеры развёрток тел».
Учащимся предлагается привести примеры реальных объектов, имеющих форму соответствующей фигуры (параллелепипед, пирамида, цилиндр, конус, шар).
6. Задача-структурирование (линейное, иерархическое, таблица) ориентирована на преобразование информации по структуре с целью получения новой информации об объекте изучения, раскрытия новых связей между элементами объекта.
Пример. Алгебра, 11-й класс. Тема «Показательные уравнения».
Задание. Соотнесите уравнения с методами их решения. Решите их и заполните таблицу.
| Метод решения | Уравнение | Корни уравнения | |
| 1 | Приведение обеих частей уравнения к одному основанию | ||
| 2 | Вынесение общего множителя за скобки | ||
| 3 | Введение новой переменной | ||
| 4 | Однородные | ||
| 5 | Показательно-степенные | ||
| 6 | Основания взаимно обратные числа | ||
| 7 | Функциональный метод |
7. Задача-возможность направлена на оценивание достоверности информации – установления истинности или ложности утверждений и существования или несуществования объектов.
Пример. Геометрия, 7-й класс. Тема «Аксиома параллельных прямых».
Задание. Прочитай задачу 2 на странице 97 учебника, поработай корректором и найди ошибки в доказательстве [1].
Задача 2.
Доказать, что если сумма внутренних односторонних углов при двух данных прямых и секущей меньше 180°, то эти прямые пересекаются.
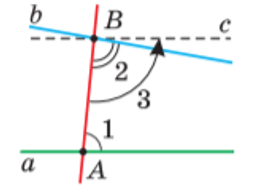Доказательство. Пусть a и b – данные прямые, AB – их секущая, сумма углов 1 и 2 меньше 180°. Отложим от луча AB угол 3, который в сумме с углом 1 дает 180°. Получим прямую c, которая параллельна прямой a по признаку параллельности прямых. Предположим, что прямые a и b не пересекаются, а, значит, параллельны. Тогда через точку A будут проходить две прямые b и c, которые параллельны прямой a. Это противоречит аксиоме параллельных прямых. Следовательно, прямые a и b пересекаются.
Работа с ошибками:
– первый вариант исправления ошибок – исправление в тексте:
1) «Отложим от луча AB угол 3», изменить на «Отложим от луча ВА угол 3»;
2) «Тогда через точку A будут проходить две прямые b и c», изменить на «Тогда через точку В будут проходить две прямые b и c».
– второй вариант исправления ошибок – исправление на чертеже: точки А и В следует поменять местами.
8. Задача на избыточность предполагает использование приема сжатия для оценивания информации на полноту.
Пример. Геометрия, 8-й класс. Тема «Площадь квадрата, прямоугольника».
Задача 1. В прямоугольнике стороны равны 8,5 см и 4 см, а периметр 25 см. Найти площадь прямоугольника.
Существует несколько вариантов выделения лишнего данного в условии задачи. Избыточным данным можно считать одну из сторон прямоугольника или его периметр. Для вычисления площади прямоугольника нужны длины соседних сторон, а они даны в условии, тогда периметр можно считать лишним данным, то есть условие задачи избыточно.
Однако следует обратить внимание учащихся на то, что избыточные данные помогают оценить корректность задачи. Для этого можно предложить следующую задачу.
Задача 2. В прямоугольнике длины сторон равны 6,5 см и 4 см, а площадь равна 25,3 см2. Найти периметр прямоугольника.
Вывод: площадь – лишнее данное. Однако прямоугольник с такими сторонами не может иметь площадь 25,3 см2. То есть, формально «решив» задачу: (6,5 + 4)·2 = 21 (см), учащиеся не учли, что площадь этого прямоугольника равна 26 см2. Следовательно, данная задача решения не имеет в силу противоречивости условия, то есть условие этой задачи не только избыточно, но и противоречиво.
После этого следует рассмотреть еще раз задачу 1 на предмет корректности условия.
9. Задача на недостаточность связана с использованием приема дополнения данных в ходе оценивания полноты информации.
С задачами такого вида может быть два варианта работы:
1) из-за недостатка условий в задаче нельзя указать однозначный ответ;
2) задачу дополняют недостающим данным и далее осуществляют поиск ее решения, рассматривая данную задачу как стандартную.
Пример. Геометрия, 8-й класс. Тема «Теорема Пифагора».
Задание. На доске был чертеж и краткая запись: АВ = 10, AС = ВC = 13, АD = ВD =7. Определите CD. Чертеж случайно стерли. Восстановите чертеж и получите ответ на вопрос задачи.
Данная задача не имеет однозначного ответа, так как не указано местоположение точки D (точки С и D могут располагаться в разных полуплоскостях относительно прямой АВ либо в одной полуплоскости).
Задачи 7-го, 8-го и 9-го типов необходимы, чтобы умение проверять достоверность предлагаемой информации, видеть в ней пробелы стало составляющим субъектного опыта учащихся.
Таким образом, современное математическое образование должно быть нацелено не столько на ознакомление учащихся с математическими понятиями, теоремами, формулами, сколько на формирование ключевых компетенций, необходимых для продуктивной аналитической, исследовательской, проектной работы в различных сферах познания.
Список источников
1 Геометрия : учеб. пособие для 7-го кл. учреждений общ. сред. образования с рус. яз. обучения / В.В.Казаков. – Минск : Народная асвета, 2017. – 173 с. : ил.
2 Герасимов, В.Д. Математика : учеб. пособие для 5-го кл. учреждений общ. сред. образования с рус. яз. обучения. В 2 ч. Ч. 1 / В.Д.Герасимов, О.Н.Пирютко, А.П.Лобанов. – Минск : Адукацыя i выхаванне, 2017. – 168 с. : ил.
3 Компетентностно-ориентированные задания в системе высшего образования / А.А.Шехонин [и др.]. – СПб : НИУ ИТМО, 2014. – 98 с.
4 Пойа, Дж. Математическое открытие. – М. : Наука, 1970. – 456 с.
5 Тришина С.В. Информационная компетентность как педагогическая категория [Электронный ресурс] / С.В.Тришина // Эйдос. – 2005. – 10 сент. – Режим доступа: http://www.eidos.ru/journal/2005/0910-11.htm. – Дата доступа: 10.09.2017 г.
Предложить публикацию