Всевозможные по содержанию задачи, которые решаются в разных темах и в разное время, объединяются и решаются вместе. В материале выбраны задачи, решение которых сводится к решению неравенств. За основу можно было взять любое неравенство, которое изучается в школьном курсе математики. Здесь автор остановилась на квадратных неравенствах.
Ольга ПЕТРУКОВИЧ,
учитель математики
ГУО «Погост-Загородская средняя школа
имени славянских просветителей Кирилла и Мефодия»
Пинского района,
Брестская область
Рассмотрим один из способов организации повторения математики за курс средней школы. Всевозможные по содержанию задачи, которые решаются в разных темах и в разное время, объединяются и решаются вместе.
Выберем задачи, решение которых сводится к решению неравенств. За основу можно было взять любое неравенство, которое изучается в школьном курсе математики. В этой статье остановимся на квадратных неравенствах.
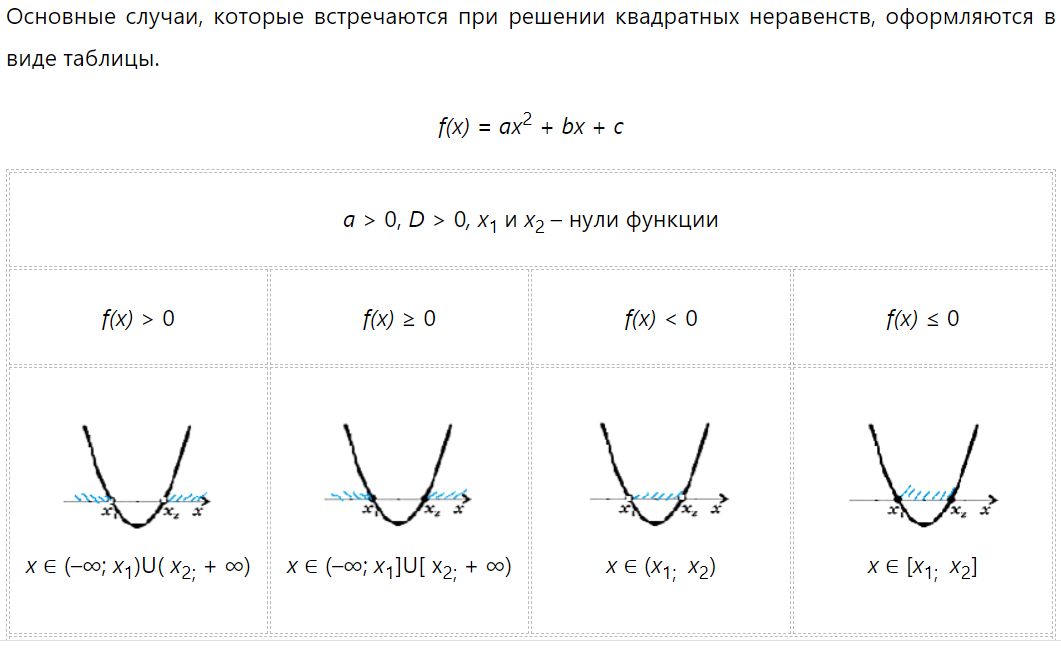
Основные случаи, которые встречаются при решении квадратных неравенств, оформляются в виде таблицы.
f(x) = ах2 + bх + с
|
а > 0, D > 0, х1 и х2 – нули функции |
|||
|
f(x) > 0 |
f(x) ≥ 0 |
f(x) < 0 |
f(x) ≤ 0 |
|
|
|
|
|
|
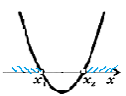
а > 0, D = 0, х1 – нуль функции |
|||
|
|
|
|
|
|
а > 0, D < 0, функция нулей не имеет |
|||
|
|
|
|
|
|
а < 0, D > 0, х1 и х2 – нули функции |
|||
|
|
|
|
|
|
а < 0, D = 0, х1 – нуль функции |
|||
|
|
|
|
|
|
а < 0, D < 0, функция нулей не имеет |
|||
|
|
|
|
|
Подробно решаем неравенства, которые будем использовать на уроках повторения (опорные неравенства).
Решить неравенство:
а) х2 – 2 х – 48 > 0;
б) х2 – 2х – 48 ≥ 0;
в) х2 – 2х – 48 < 0;
г) х2 – 2х – 48 ≤ 0.
Алгоритм решения для всех неравенств один и тот же. Он отличается только поиском ответа. Поэтому сначала напишем общую часть алгоритма для всех случаев.
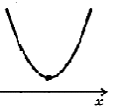
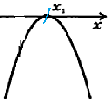
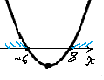
1. Рассмотрим функцию у= х2 –2х – 48 – квадратичная функция, график – парабола, ветви направлены вверх (а = 1 > 0). D = R.
2. Найдем нули функции. у= 0, если х2– 2х – 48 = 0.
а = 1, b = –2, с = – 48
D = b2 – 4ас = (–2)2– 4·1·(–48) = 196 > 0, два нуля. Значит, парабола пересекает ось абсцисс в двух точках. √ D = 14.
х1 = (–b – √ D) : (2а) = (2 – 14) : (2·1) = –6,
х2 = (–b + √ D) : (2а) = (2 + 14) : (2·1) = 8.
3. Схематически покажем график и найдем решение неравенства (поиск ответа для каждого случая).
|
|
|
|
|
Перечень задач, для решения которых используются квадратные неравенства
|
Тема |
Типы задач |
|
Выражения с переменной |
– Найдите область определения выражения. |
|
Функции |
– Найдите область определения функции |
|
Уравнения |
– Решить уравнение │f(x)│ = f(x) |
|
Текстовые задачи |
Решить задачу |
|
Неравенства и их системы |
– Решите квадратное неравенство |
Примеры задач, для решения которых используются квадратные неравенства
Выражения с переменной
Задача 1. При каких натуральных значениях переменной выражение х2 – 2х – 48 принимает неположительные значения?
Решение. Составим неравенство, учитывая условие задачи. Имеем
х2 – 2х –48 ≤ 0.
Получили опорное неравенство г) х2 – 2х – 48 ≤ 0

х ∈ [–6; 8].
Учитывая, что нужно найти натуральные значения переменной, приходим к такому решению: х ∈ {1, 2, 3, 4, 5, 6, 7, 8}.
Ответ: {1, 2, 3, 4, 5, 6, 7, 8}
Задача 2. Найдите, при каких значениях переменной выражение √ х2 – 2х –48 не имеет смысла.
Решение. Так как арифметический квадратный корень имеет смысл для всех неотрицательных значений подкоренного выражения, то выражение
√ х2 – 2х – 48 не имеет смысла, если х2 – 2х – 48 < 0.
Получили опорное неравенство в) х2 – 2х – 48 < 0

х ∈ (–6; 8).
Ответ: (–6; 8)
Функция
Задача 1. Найдите область определения функции y = log7(х2 – 2х – 48).
Решение. Область определения логарифмической функции состоит из всех значений переменной, при которых подлогарифмическое выражение принимает только положительные значения.
Имеем неравенство: х2 – 2х – 48 > 0.
Пришли к опорной задаче а) х2 – 2х – 48 > 0.

х ∈ (–∞; –6)U(8; + ∞).
Ответ: D(f) = (–∞; –6)U(8; + ∞).
Задача 2. При каких значениях аргумента функция y = (–х4 –10) (х2 – 2х – 48) принимает отрицательные значения.
Решение. Так как первый множитель принимает отрицательные значения для всех значений аргумента, то произведение будет отрицательным, если второй множитель принимает положительные значения. Т. е. х2 – 2х – 48 > 0.
Пришли к опорной задаче а) х2 – 2х – 48 > 0.

х ∈ (–∞; –6)U(8; + ∞).
Ответ: (–∞; –6)U(8; + ∞).
Уравнения
Задача 1. Решите уравнение │х2 – 2х – 48│ = х2 – 2х – 48.
Решение. Так как │а│ = а, если а ≥ 0, то от уравнения перейдем к неравенству х2 – 2х – 48 ≥ 0.
Получили опорное неравенство б) х2 – 2х – 48 ≥ 0.

х ∈ (–∞; –6]U[8; + ∞).
Ответ: (–∞; –6]U[8; + ∞).
Задача 2. Найдите все значения параметра (буквы t), при которых квадратное уравнение 0,5х2 – tх + t + 24 = 0 не имеет корней.
Решение. Квадратное уравнение не имеет корней, если дискриминант принимает отрицательные значения, т. е D < 0. Найдем дискриминант уравнения.
а = 0,5; b = –t; с = t + 24.
D = b2–4ас = (–t)2– 4·0,5·( t + 24) = t2 – 2t – 48.
Составим неравенство t2 – 2t – 48 < 0.
Получили опорное неравенство в) х2 –2х –48 < 0.

t ∈ (–6; 8).
Ответ: (–6; 8).
Текстовые задачи
Задача. Прибывших на парад солдат планировали построить так, чтобы в каждом ряду стояло по 24 человека. Но не все прибывшие смогли участвовать в параде, и их перестроили так, что число рядов стало на 2 меньше, а число человек в ряду на 26 больше нового числа рядов. Если бы все солдаты участвовали в параде, то их можно было бы построить так, чтобы число рядов было равно числу человек в ряду. Сколько солдат прибыло на парад?
Решение. х – первоначальное число рядов,
тогда 24х – число прибывших солдат.
х – 2 – число рядов после перестроения,
(х – 2) + 26 = х + 24 (– число солдат в ряду после перестроения.
Тогда (х –2)(х + 24) – число солдат после перестроения.
Чтобы решить задачу, можно составить следующее неравенство. Так как число солдат после перестроения меньше первоначального, имеем (х –2 )(х + 24) < 24х .
Раскроем скобки, приведем подобные и приходим к опорной задаче
в) х2 – 2х – 48 < 0.

х ∈ (– 6; 8).
Учитывая, что число рядов может быть только натуральным числом, решения ограничиваются числами от 1 до 7, включая эти числа. Если учесть еще и последнее предположение о перестроении квадратом (число человек в ряду равно числу рядов), то получаем произведение двух одинаковых чисел. Это значит, что из первоначального числа солдат (24х) должен извлекаться квадратный корень.
Проверяем. х = 1, то 24 * 1 = 24 – число не является точным квадратом;
х = 2, то 24 * 2 = 48 – число не является точным квадратом;
х = 3, то 24 * 3 = 72 – число не является точным квадратом;
х = 4, то 24 * 4 = 96 – число не является точным квадратом;
х = 5, то 24 * 5 = 120 – число не является точным квадратом;
х = 6, то 24 * 6 = 144 – число является точным квадратом;
х = 7, то 24 * 7 = 168 – число не является точным квадратом;
Единственное число, удовлетворяющее предположению, это х = 6. Следовательно, число солдат равно 144.
Ответ: 144.
Неравенства
Задача 1. Решите неравенство (х2 + 4)/(√ (х2 –2х –48)) ≥ 0.
Решение. Так как числитель принимает только положительные значения, то дробь будет неотрицательной, если знаменатель положительный (знаменатель не равен нулю, т. к. на ноль делить нельзя). Получаем неравенство √(х2 – 2х – 48) > 0. Арифметический квадратный корень больше нуля для всех значений переменной из области определения, кроме нуля. Имеем
х2 – 2х – 48 > 0.
Пришли к опорной задаче а) х2 – 2х – 48 > 0.

х ∈ (–∞; –6)U(8; + ∞).
Ответ: (–∞; –6)U(8; + ∞).
В заключении еще раз хочется отметить, что такая работа позволяет видеть за всевозможными формами, число которых велико, задачи, решаемые по одной схеме. Решение таких задач отличается только первым шагом или совершенно одинаково. Такая систематизация математических задач позволяет сузить их многообразие, упростить подготовку к экзамену по математике.

























 Предложить публикацию
Предложить публикацию