Рэалізацыя выхаваўчага патэнцыялу ўрока на прыкладзе ўрока матэматыкі ў 8-м класе па тэме “Формулы каранёў квадратнага ўраўнення”

Людміла ЗАЯЦ,
настаўнік матэматыкі
ДУА “Азёркаўская сярэдняя школа”
Мастоўскага раёна,
Гродзенская вобласць

Тэма: «Формулы каранёў квадратнага ўраўнення».

Мэта ўрока: стварэнне ўмоў для абагульнення і сістэматызацыі ведаў па тэме “Формулы каранёў квадратнага ўраўнення”.

Задачы ўрока

Адукацыйная: арганізаваць дзейнасць вучняў, накіраваную на абагульненне і сістэматызацыю ведаў, уменне рашаць квадратныя ўраўненні па формуле;

Развіваючая: садзейнічаць развіццю пазнавальных навыкаў, лагічнага мыслення, памяці, тэхнікі вылічэння, умення правяраць і ацэньваць выкананую работу, навыкаў калектыўнай працы ў спалучэнні з індывідуальнай;

Выхаваўчая: стварыць умовы для выхавання ўмення працаваць з інфармацыяй у прапанаваных умовах, станоўчага матыву да вучобы, добрасумленных адносін да працы, дысцыплінаванасці, адказнасці за вынікі сваёй работы, выхаванне пачуцця калектывізму.

Тып урока: урок замацавання і развіцця ведаў, уменняў, навыкаў.

Абсталяванне: прэзентацыя, карткі з тэстам, карткі з дадатковымі заданнямі і ўраўненнямі, карткі з рэфлексіяй.

Ход урока

І Арганізацыйны момант. Стварэнне псіхалагічнага настрою

– Добры дзень! Сядайце! А зараз, для таго каб на працягу ўсёй нашай з вамі працы панавала атмасфера добразычлівасці, я прапаную вам выканаць наступныя дзеянні:

– Папляскайце ў далоні тыя, у каго зараз добры, бадзёры настрой.

– Пацісніце руку суседу, калі вы добры чалавек і гатовыя дапамагчы таварышам.

– Усміхніцеся адно аднаму, хто сёння будзе ўважлівым і старанным.

– Я жадаю вам добрага настрою і поспехаў на ўроку! Зараз, я спадзяюся, вы настроены на работу, і мы можам з вамі пачынаць.

ІІ Матывацыйны этап. Пастаноўка мэты ўрока

– Сёння мы правядзём урок абагульнення і сістэматызацыі ведаў па тэме “Формулы каранёў квадратнага ўраўнення”. Вы ўжо дастаткова добра ведаеце гэту тэму і ўмееце рашаць ураўненні па ёй. Таму наша з вамі задача: … (Адказы вучняў).

– Правільна: абагульніць і скласці ў сістэму ўсе тыя веды і ўменні, якімі вы валодаеце пры рашэнні квадратных ураўненняў.

– Ураўненні з даўніх часоў хвалявалі розум чалавецтва. Па гэтай прычыне ў англійскага паэта сярэдніх вякоў Чосэра ёсць выдатныя радкі, якія я прапаную зрабіць эпіграфам нашага ўрока:

Посредством уравнений, теорем
Я уйму всяких разрешил проблем.

– Рашэнне квадратных ураўненняў таксама не выключэнне. Яны вельмі важныя і для матэматыкі, і для іншых навук, напрыклад, фізікі. А ці задумваліся вы, чаму так? Аказваецца, уменне рашаць ураўненні мае не толькі вялікае значэнне для дасканалага ведання матэматыкі і яе законаў, але гэтыя веды спатрэбяцца вам і на практыцы. Амаль штодзённа нам даводзіцца сутыкацца з рознымі праблемамі, дзе ніяк не абысціся без рашэння розных відаў ураўненняў. Навучыўшыся іх рашаць і авалодаўшы іх спосабамі рашэння, у далейшым вы зможаце лёгка знайсці адказы ў любой галіне навукі і тэхнікі. А ўменне разумець і рашаць квадратныя ўраўненні з’яўляецца падмуркам да засваення ведаў матэматычных навук. На наступных уроках матэматыкі вам прыйдзецца рашаць тэкставыя задачы, і вось тут неабходна будзе ўмець хутка і правільна спраўляцца з рашэннем квадратных ураўненняў.

– Прымяненне квадратных ураўненняў у жыцці можна ўбачыць на малюнку

– А сённяшні ўрок пакажа, наколькі вы гатовы крочыць па ступеньках матэматыкі далей. Я спадзяюся, што вы будзеце актыўна працаваць на ўроку.

ІІІ Праверка дамашняга задання

Франтальнае апытванне класа.

IV Актуалізацыя апорных ведаў

– Каб настроіцца на работу і паўтарыць тэарэтычны матэрыял, пачнём з невялікай размінкі. Паўторым матэматычныя тэрміны, звязаныя з рашэннем квадратных ураўненняў.

Самастойнае выкананне заданняў з самаправеркай

1) Як называецца ўраўненне выгляду  , дзе x – зменная, a, b і с – некаторыя лікі, прычым а0? (Квадратнае)

2) Як называецца квадратнае ўраўненне, у якога хаця б адзін з яго каэфіцыентаў b або с роўны нулю? (Няпоўнае)

3) Значэнне зменнай, пры якой ураўненне пераўтвараецца ў правільную лікавую роўнасць называецца… (Корань)

4) Квадратнае ўраўненне, у якім каэфіцыент а роўны 1 называецца… (Прыведзеным)

5) Як называецца выраз  для квадратнага ўраўнення? (Дыскрымінант)

6) Калі дыскрымінант роўны нулю, то ўраўненне мае колькі каранёў? (Адзін)

7) Калі дыскрымінант больш нуля, то ўраўненне мае колькі каранёў? (Два)

Самаправерка па адказах на экране камп’ютара.

Тэст “Віды квадратных ураўненняў”

– Зараз давайце праверым, наколькі добра вы ўмееце вызначаць віды квадратных ураўненняў. Вашай увазе прапануецца тэст, у якім запісана пяць ураўненняў. Насупраць кожнай калонкі вы ставіце плюс, калі яно належыць да дадзенага выгляду.

Ключ да тэсту

Вучні мяняюцца лісточкамі і па ключы правяраюць адказы, ацэньваючы работу таварыша. Вынік запісваецца ў калонку “ацэначны бал”, адно заданне – 2 балы.

V Аперацыйны этап

– А цяпер прыступім да практычнай часткі нашага ўрока. Паўтарылі асноўныя паняцці тэмы, а зараз праверым, як яны “працуюць” у практычных заданнях.

Набываць веды – адвага,
Памнажаць іх – мудрасць,
А ўмела ўжываць – вялікае мастацтва.

“Знайдзі памылку” (работа ў парах)

– Пры рашэнні квадратных ураўненняў мы часта дапускаем памылкі або па няўважлівасці, або па няведанні. Вам у парах патрэбна знайсці памылкі, якія дапушчаны пры рашэнні квадратных ураўненняў.

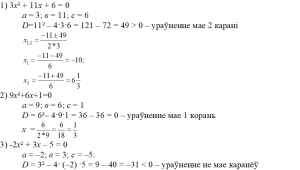
“Цікава ведаць”

– Ці не цікава вам ведаць, калі людзі навучыліся рашаць квадратныя ўраўненні?

– Простыя ўраўненні людзі навучыліся рашаць болей як тры тысячы гадоў назад у Старажытным Егіпце, Вавілоне. І толькі рашыўшы ўраўненне у² – 8у + 16 = 0, мы даведаемся, у якім стагоддзі да нашай эры людзі навучыліся рашаць квадратныя ўраўненні.

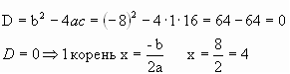
– Гэта значыць, што ў ІV стагоддзі да нашай эры людзі навучыліся рашаць квадратныя ўраўненні. Малайцы! Усе справіліся з гэтым заданнем, добра папрацавалі, і я прапаную вам адпачыць.

3 Фізкультмінутка

– Зараз мы з вамі зробім размінку для вачэй. Так як на вуліцы ў нас зараз зіма, я вам прапаную ўявіць сняжынку і прасачыць за яе палётам зверху ўніз. Паўтарыце практыкаванне некалькі разоў.

– Затым паднялася мяцеліца – сняжынка закружылася ў паветры, прасачыце за яе палётам. Паўтарыце практыкаванне некалькі разоў.

4 Практычная частка

Адпрацоўка навыкаў і ўменняў рашаць квадратныя ўраўненні

– Патрэбна запоўніць пустыя ячэйкі табліцы з дапамогай складоў, якія ў вас атрымаюцца пры рашэнні квадратных ураўненняў.

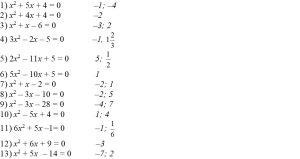
Вучні рашаюць пранумараваныя квадратныя ўраўненні ў сшытках. На дошцы знаходзяцца карткі з адказамі.

– Калі знойдзеце картку са сваім адказам, то змясціце яе ў адпаведную ячэйку.

Вучні, якія справіліся з заданнем, становяцца кансультантамі і дапамагаюць астатнім.

– Такім чынам, мы атрымалі выказванне Я.А.Каменскага: “Вучыцца нялёгка, але цікава!” Я думаю, гэтыя словы як найлепш, падыходзяць да нашага ўрока.

VI Вынікі ўрока. Выстаўленне і каменціраванне адзнак

– Якую мэту мы паставілі ў пачатку ўрока?

– Ці дасягнулі мы яе?

– На што неабходна звярнуць увагу дома пры рабоце над гэтай тэмай?

VII Рэфлексія

Вучні фіксуюць самаацэнку сваёй дзейнасці:

– калі яны задаволены вынікам сваёй дзейнасці, то паднімаюць зялёны прамавугольнік,

– калі задаволены, але маглі б лепш – то жоўты,

– калі незадаволены – то чырвоны.

VII Дамашняе заданне

Карткі з заданнямі (па ўзроўнях).

Поделиться ссылкой: