Сродкам развіцця пазнавальнай актыўнасці вучняў, павышэння іх матывацыі на ўроках матэматыкі, безумоўна, з’яўляецца выкарыстанне ў навучальным працэсе практыка-арыентаваных задач і задач з міжпрадметным зместам, што садзейнічае росту ўнутранай матывацыі вучняў да вывучэння прадмета.
Марына ІГНАЦІК,
настаўнік матэматыкі
ДУА “Дварэцкая сярэдняя школа”
Дзятлаўскага раёна,
Гродзенская вобласць
У цяперашні час для таго каб паспяхова жыць, развіваць і рэалізоўваць свае здольнасці ў свеце, які пастаянна змяняецца і насычаецца праблемамі, чалавеку неабходна валодаць не толькі трывалымі ведамі, але і ўстойлівым імкненнем да сталай самаадукацыі, уменнем перавучвацца ў залежнасці ад патрабаванняў рынку і сацыяльных патрэбнасцей, прымяняць атрыманыя веды на практыцы.
Педагагічная практыка паказвае, што неабходнай умовай асобаснага развіцця вучняў у гэтым напрамку з’яўляецца актывізацыя іх пазнавальнай дзейнасці. У сваю чаргу, узровень пазнавальнай актыўнасці вучняў напрамую залежыць ад разумення імі неабходнасці і практычнай значнасці ведаў. Так, калі прадмет матэматыкі, які вывучаецца, не звязаны з практыкай, ён уяўляецца вучням дарэмным завучваннем формул, тэарэм і разліковых алгарытмаў.
Сродкам развіцця пазнавальнай актыўнасці вучняў, павышэння іх матывацыі на ўроках матэматыкі, безумоўна, з’яўляецца выкарыстанне ў навучальным працэсе практыка-арыентаваных задач і задач з міжпрадметным зместам, што садзейнічае росту ўнутранай матывацыі вучняў да вывучэння прадмета; выхаванню сацыяльна мабільнай асобы, якая мае жаданне і імкненне пазнаваць, здольная планаваць і арганізоўваць сваю вучэбную дзейнасць, ставіць і дасягаць мэты, аналізаваць атрыманы вынік; прымяняць атрыманыя веды да вырашэння жыццёвых практычных сітуацый, што неабходна для паспяховай сацыялізацыі і самарэалізацыі.
Мэты ўрока:
– адукацыйная – навучыцца прымяняць веды, уменні і навыкі, набытыя пры вывучэнні раздзела “Сума вуглоў трохвугольніка” да рашэння практыка-арыентаваных задач і задач з міжпрадметным зместам;
– развіваючая – развіваць актыўнасць і цікавасць вучняў да пазнаваўчай дзейнасці, усведамленне значнасці матэматыкі для розных сфер дзейнасці і гатоўнасці да выкарыстання матэматычных ведаў у паўсядзённым жыцці;
– выхаваўчая – выхоўваць якасці асобы, якія забяспечваюць сацыяльную мабільнасць: здольнасць самастойна ставіць і дасягаць мэты, прымаць рашэнні і аргументавана адстойваць свае перакананні, аб’ектыўна ацэньваць вынік сваёй работы.
Прагназуемы вынік дзейнасці вучняў: на працягу ўрока вучні атрымаюць магчымасць удасканаліць навыкі бачыць у жыццёвых практычных задачах матэматычны змест, перакладаць практыка-арыентаваную задачу на мову матэматыкі, шукаць і знаходзіць яе рацыянальныя спосабы рашэння; у канцы ўрока змогуць выканаць прапанаваныя ім заданні па тэме ў якасці кантролю ведаў.
Тып урока: урок прымянення ведаў і ўменняў.
Абсталяванне і матэрыялы: мультыборд, раздатачны матэрыял.
Ход урока
1 Арганізацыйна-матывацыйны этап (1 мінута)
Мэта этапа: стварыць у класе камфортную эмацыянальную атмасферу, настроіць вучняў на прадуктыўную вучэбную дзейнасць.
– Добры дзень. Спадзяюся, вы ў добрым настроі. Пачнём наш урок з філасофскай загадкі Вальтэра (дэманстрацыя на мультыбордзе): “Што самае хуткае, але і самае павольнае, самае вялікае, але і самае маленькае, самае працяглае і кароткае, самае дарагое і тое, што не вельмі намі шануецца?” (Час.)
– У нас усяго 45 мінут, і мне б вельмі хацелася, каб гэты час вы скарысталі з карысцю.
2 Этап пастаноўкі вучэбных задач (1,5 мінуты)
Мэта этапа: стварыць умовы для ўсведамлення і прыняцця вучнямі мэты вучэбнай дзейнасці.
– Тэма нашага ўрока: “Практыка-арыентаваныя задачы, задачы з міжпрадметным зместам і іх рашэнне”(на дошцы). Якія задачы маюцца на ўвазе? (Задачы, навыкі рашэння якіх нам спатрэбіцца ў жыцці.)
– Так. Таксама гэта задачы, якія даказваюць жыццёвую неабходнасць ведаў, што набываюцца ў школе, дапамагаюць зразумець непасрэдную сувязь вывучэння матэматыкі з практычнай дзейнасцю чалавека. Як звычайна, такім задачам мы прысвячаем цэлыя ўрокі напрыканцы вывучэння раздзела. Назавіце тэму раздзела, які мы вывучаем, і паспрабуйце сфармуляваць вучэбныя задачы на сённяшні ўрок. (Нам неабходна навучыцца прымяняць веды, уменні і навыкі, набытыя пры вывучэнні раздзела “Сума вуглоў трохвугольніка”, да рашэння практыка-арыентаваных задач і задач з міжпрадметным зместам.)
3 Этап актуалізацыі апорных ведаў (4 мінуты)Мэта этапа: стварыць умовы для канцэнтрацыі ўвагі на навучальным матэрыяле і актывізацыі разумовай дзейнасці, аператыўнага прымянення ведаў; праверыць тэарэтычную гатоўнасць вучняў да ўрока, выявіць індывідуальныя цяжкасці.Арганізацыя паўтарэння вывучанага матэрыялу на працягу года (трохвугольнік, віды трохвугольнікаў, перыметр трохвугольніка).
Рашэнне задачы (раздатачны матэрыял, дэманстрацыя на мультыбордзе).
(А.Н.Пірутка, В.В.Казакоў і інш. Кампетэнтнасны падыход. Матэматыка. 7–9 класы. Дыдактычныя і дыягнастычныя матэрыялы.)
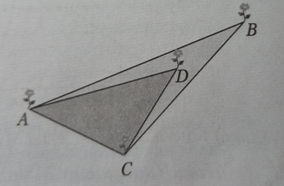
Кветнік мае форму раўнабедранага трохвугольніка АВС з перыметрам 18 м. На яго аснове АС унутры клумбы разбіта іншая клумба ў форме роўнастаронняга трохвугольніка АDС з перыметрам 12 м, як паказана на малюнку. Па перыметрам раўнабедранага і роўнастаронняга трохвугольнікаў трэба высадзіць кветкі з інтэрвалам 20 см. Колькі кветак будзе высаджана па старане АВ? Ці хопіць 90 руб. на добраўпарадкаванне такога кветніка, калі плата за работу складае 25 руб. і адна кветка каштуе 50 кап.?
Вучні па чарзе паэтапна рашаюць задачу. (Адказ: хопіць).
4 Этап праверкі дамашняга задання (6 мінут)
Мэта этапа: выявіць ступень разумення навучальнага матэрыялу, індывідуальныя цяжкасці, садзейнічаць развіццю навыкаў самааналізу, стварыць умовы для захавання матывацыі рэгулярна і якасна выконваць дамашняе заданне.
(Адзін з вучняў каля дошкі тлумачыць ход рашэння дамашняй задачы (№ 245*) па гатовым чарцяжы, паведамляе прамежкавыя вынікі вылічэнняў і выніковы адказ. Вучні ўважліва слухаюць, пры неабходнасці выпраўляюць памылкі, указваюць на недакладнасці ў адказе аднакласніка, задаюць удакладняючыя пытанні).
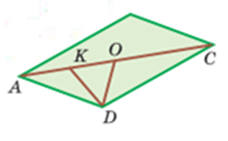
На малюнку адлюстраваны зялёны газон, які мае форму прамавугольніка (рыс. 283). Дарожка АС утварае вугал 30° са стараной DC, дарожка DO праходзіць праз сярэдзіну дарожкі АС. Дарожка DK перпендыкулярная дарожцы АС. Адлегласць КО роўна 8 м. Знайдзіце даўжыню дэкаратыўнага плота, які агароджвае трохвугольны ўчастак АОД.
Адказ: 48 м.
(Апорныя веды: адлегласць ад пункта да прамой, раўнабедраны і роўнастаронні трохвугольнік, уласцівасці раўнабедранага і роўнастаронняга трохвугольніка, тэарэма аб катэце, які ляжыць насупраць вугла 30°).
(Аднаму з вучняў у гэты час прапануецца дадатковае індывідуальнае заданне – задача з раздзела “Рэальная геаметрыя”, падручнік, с .119). (Адказ: 40°).
(Апорныя веды: разгорнуты вугал, прамавугольны трохвугольнік, сума вострых вуглоў прамавугольнага трохвугольніка).
Дадатковыя пытанні:
– Сувязь з якім прадметам адлюстроўвае дадзеная задача? (Фізіка.)
– Які матэрыял выкарыстоўваецца пры рашэнні дадзенай задачы? (Закон фізікі: вугал падзення роўны вуглу адбіцця.)
– Які вывад можна зрабіць з задачы згодна дадзенаму закону? (Вугал паміж траекторыяй пасланай шайбы і бортам роўны вуглу паміж траекторыяй адбітай шайбы і гэтым бортам.)
Дадатковы матэрыял, падрыхтаваны вучнем (на мультыбордзе дэманструецца некалькі слайдаў, суправаджаючых выступленне вучня):
У Рэспубліцы Беларусь вялікая ўвага надаецца папулярызацыі хакея. Пры ўдзеле Прэзідэнцкага спартыўнага клуба праходзіць рэспубліканскі турнір аматарскіх падлеткавых каманд “Залатая шайба”, міжнародны Калядны турнір на прыз Прэзідэнта Рэспублікі Беларусь. У рэйтынгу Міжнароднай федэрацыі хакея нацыянальная зборная Беларусі знаходзіцца ў дзясятцы лепшых каманд свету.
5 Этап рашэння задач. (20 мінут)
Мэта этапа: арганізаваць пазнавальную дзейнасць праз рашэнне практыка-арыентаваных задач, стымуляваць праяву творчай актыўнасці вучняў да самарэалізацыі і самаразвіцця.
Задача № 1 (раздатачны матэрыял, дэманстрацыя на мультыбордзе).
(Заданне рэспубліканскага маніторынгу ўзроўню навучанасці вучняў VІІІ класа па вучэбным прадмеце “Матэматыка”, варыянт 1)
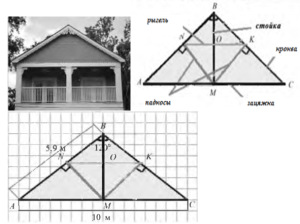
На фотаздымку – жылы дом. Дах – важны элемент жылога дома, які абараняе яго ад знешніх уздзеянняў.
На малюнку паказана матэматычная мадэль франтона (франтон – трохвугольная частка фасада дома), распрацаваная цесляром, а таксама паказаны даўжыні некаторых адрэзкаў і градусныя меры вуглоў. Кроквы даху (адрэзкі АВ і ВС) з’яўляюцца бакавымі старанамі раўнабедранага трохвугольніка АВС, зацяжка (адрэзак АС) – аснова трохвугольніка АВС.
Важнымі элементамі даху з’яўляюцца: стойка (адрэзак ВМ) – перпендыкуляр, праведзены з пункта В да прамой АС, рыгель (адрэзак NK) і падкосы (адрэзкі МN і МK), каторыя неабходны для надання ўстойлівасці ўсёй канструкцыі.
Вядома, што даўжыня адной з крокваў даху (адрэзка АВ трохвугольніка АВС) – 5,9 м, даўжыня зацяжкі (адрэзка АС) – 10 м; вугал паміж кроквамі (вугал АВС) роўны 120°. Пункт М – сярэдзіна стараны АС трохвугольніка АВС; АС // NK.
1.1. Вызначце від франтона (трохвугольніка АВС).
1.2. Вызначце вугал паміж кроквай і стойкай (вугал АВМ), калі адрэзак ВМ – бісектрыса трохвугольніка АВС.
1.3. Вызначце даўжыню другой кроквы (адрэзка ВС).
1.4. Ці роўныя вугал паміж рыгелем і падкосам (вугал NКМ) і вугал паміж падкосам і зацяжкай (вуглу КМС)? Калі так, то чаму?
1.5. Вызначце суму вуглоў пры аснове трохвугольніка АВС.
1.6. Знайдзіце вугал паміж кроквай і зацяжкай (вугал ВСА) і вугал паміж кроквай і рыгелем (вугал ВКN).
Вучні па чарзе паэтапна рашаюць задачу.
Адказы:
1.1. трохвугольнік АВС – раўнабедраны;
1.2. вугал АВМ роўны 60°;
1.3. ВС = 5,9м;
1.4. вугал NКМ роўны вуглу КМС (60°);
1.5. 60°;
1.6. 30° (вугал ВСА і вугал ВКN роўныя).
(Апорныя веды: віды трохвугольнікаў; вуглы ўтвораныя пры перасячэнні дзвюх паралельных прамых сякучай; тэарэма аб суме вуглоў трохвугольніка)
Фізкультурная хвілінка (1 мінута)
Мэта этапа: зняць разумовае і фізічнае напружанне, прадухіліць ператамленне вучняў.
Задача № 2 (раздатачны матэрыял, дэманстрацыя на мультыбордзе).
(А.Н.Пірутка, В.В.Казакоў і інш. Кампетэнтнасны падыход. Матэматыка. 7–9 класы. Дыдактычныя і дыягнастычныя матэрыялы.)
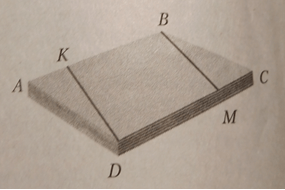
Дызайнер робіць стальніцу для стала з прамавугольнага ліста фанеры, адзначыўшы роўныя адлегласці АК = 30 см і СМ = 30 см і зрабіўшы разрэзы па прамых DК і МВ. Растлумачце, чаму дызайнер упэўнены, што процілеглыя краі атрыманай стальніцы DКВМ будуць роўныя.
(Апорныя веды: прамавугольнік; прамавугольны трохвугольнік і яго стораны; прыметы роўнасці прамавугольных трохвугольнікаў).
Задача № 3.
(Задача 2 з раздзела “Рэальная геаметрыя”, падручнік, с. 144.) Вучні па чарзе паэтапна рашаюць задачу.
Адказы:
1) вугал АВК = 30°; 2) вугал СВК = 60°; 3) вугал ВСО = 60°; 4) вугал ВОС = 60°; 5) вугал СОК = 120°, вугал ОКД = 120°; 6) перыметр трохвугольніка ВСО роўны 240 см.
(Апорныя веды: віды трохвугольнікаў; перыметр трохвугольніка; тэарэма аб сумежных вуглах; тэарэма аб суме вуглоў трохвугольніка)
6 Этап тлумачэння дамашняга задання (1,5 мінуты)
Мэта этапа: праінфармаваць вучняў аб дамашнім заданні, высветліць узровень разумення вучнямі яго зместу і спосабаў рашэння, пры неабходнасці растлумачыць методыку выканання.
Паўтарыць апорны канспект па раздзеле “Сума вуглоў трохвугольніка”(с. 145).
Задача № 3 з раздзела “Рэальная геаметрыя”, падручнік, с. 144;
дадатковае заданне – з раздзела “Мадэляванне”, падручнік, с. 144 (па жаданні).
7 Этап кантролю ведаў (5 мінут)
Мэта этапа: праверыць узровень сфарміраванасці навыку прымянення ведаў і ўменняў, набытых пры вывучэнні раздзела “Сума вуглоў трохвугольніка”, да рашэння практыка-арыентаваных задач.
(Раздатачны матэрыял).
(Заданне рэспубліканскага маніторынгу ўзроўню навучанасці вучняў VІІІ класа па вучэбным прадмеце “Матэматыка”, варыянт 2).
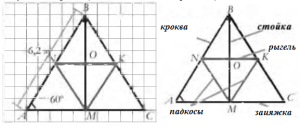
На малюнку паказана матэматычная мадэль франтона (франтон – трохвугольная частка фасада дома), распрацаваная цесляром, а таксама паказаны даўжыні некаторых адрэзкаў і градусныя меры вуглоў. Кроквы даху (адрэзкі АВ і ВС) з’яўляюцца бакавымі старанамі раўнабедранага трохвугольніка АВС, зацяжка (адрэзак АС) – аснова трохвугольніка АВС.
Важнымі элементамі даху з’яўляюцца: стойка (адрэзак ВМ) – перпендыкуляр, праведзены з пункта В да прамой АС, рыгель (адрэзак NK) і падкосы (адрэзкі NМ і МK), каторыя неабходны для надання ўстойлівасці ўсёй канструкцыі.
Вядома, што даўжыня адной з крокваў даху (адрэзка АВ трохвугольніка АВС) – 6,2м; вугал паміж кроквай і зацяжкай (вугал ВСА) роўны 60°. Пункт М – сярэдзіна стараны АС трохвугольніка АВС; АС // NK.
1.1. Вызначце від франтона (трохвугольніка АВС).
1.2. Вызначце вугал паміж кроквай і стойкай (вугал АВМ), калі адрэзак ВМ – бісектрыса трохвугольніка АВС.
1.3. Вызначце даўжыню другой кроквы (адрэзка ВС).
1.4. Ці роўныя вугал паміж рыгелем і падкосам (вугал NКМ) і вугал паміж падкосам і зацяжкай (вуглу КМС)? Калі да, то чаму?
1.5. Вызначце вугал АВС.
1.6. Знайдзіце вугал паміж кроквамі (вугал АВС) і вугал паміж кроквай і рыгелем (вугал ВКN).
Адказы:
1.1. Трохвугольнік АВС – роўнастаронні;
1.2. Вугал АВМ роўны 30°;
1.3. ВС = 6,2 м;
1.4. Вугал NКМ роўны вуглу КМС (60°);
1.5. 60°;
1.6. Вугал АВС роўны 60°, вугал ВКN роўны 60°.
Дэманстрацыя адказаў на мультыбордзе. Самаправерка.
8 Этап рэфлексіі, падвядзення вынікаў (5 мінут)
Мэта этапа: садзейнічаць развіццю навыкаў самакантролю, самаацэнкі і самакарэкцыі, стварыць умовы для развіцця творчых здольнасцей і пашырэння магчымасцей пры выкананні дамашняга задання.
Вучням прапануюцца наступныя пытанні для абмеркавання (раздатачны матэрыял):
– Якія задачы мы ставілі перад сабой у пачатку ўрока?
– Ці выканалі мы пастаўленыя перад сабой задачы?
– Ці атрымалі вы новыя веды, уменні і навыкі ў працэсе ўрока?
– Як можна іх выкарыстаць у практычнай жыццядзейнасці або будучай прафесійнай дзейнасці?
– Ці ўстанавілі мы належную сувязь матэматычных ведаў, і канкрэтна ведаў па пройдзеным раздзеле “Сума вуглоў трохвугольніка”, з практычным жыццём?
Дадаткова выкарыстоўваецца метад незакончаных сказаў:
1. Матэрыял урока быў (якім?) … (цікавым, карысным, цяжкім, пасільным, лёгкім)
2. Я даведаўся…, навучыўся…
3. Я адчуваў цяжкасці пры…
4. Я зацікавіўся…
5. Урок прымусіў мяне задумацца…
Настаўнік дае славесную ацэнку дзейнасці вучняў. Ацэньвае вучняў адзнакамі.
– Спадзяюся, што на прыкладзе сённяшняга занятку вы ў чарговы раз пераканаліся, што, калі не кожны можа стаць матэматыкам, то ў жыцці матэматыка будзе патрэбна кожнаму.



 Предложить публикацию
Предложить публикацию