 Татьяна ТУРОВЕЦ,
Татьяна ТУРОВЕЦ,
заместитель директора по учебно-воспитательной работе
ГУО «Скрыгаловская средняя школа
имени Н.И.Шляги Мозырского района»,
Гомельская область
В 9-м классе при изучении темы «Соотношения в прямоугольном треугольнике: синус, косинус, тангенс и котангенс острого угла» закладываются основы изучения одного из сложнейших разделов математики – тригонометрии. Именно по этой причине стоит обратить внимание на отработку навыков по различению понятий синус, косинус, тангенс и котангенс острого угла, определению их табличных значений.
Для запоминания и отработки навыков по определению соотношения сторон в прямоугольном треугольнике предлагаем учащимся математический тренажер, в котором необходимо по данным рисунка определить значения синуса, косинуса, тангенса и котангенса определенных углов.
Обратим внимание на то, что этот тренажер позволяет отработать предложенные в учебнике определения; выполняя задания тренажера, необходимо акцентировать внимание учащихся на повторении и проговаривании определений. Задания под номерами 9 и 10 позволяют не только опираться на определение в готовом виде, но и соотносить его с предложенным результатом, тем самым проводя анализ условия предложенного задания.
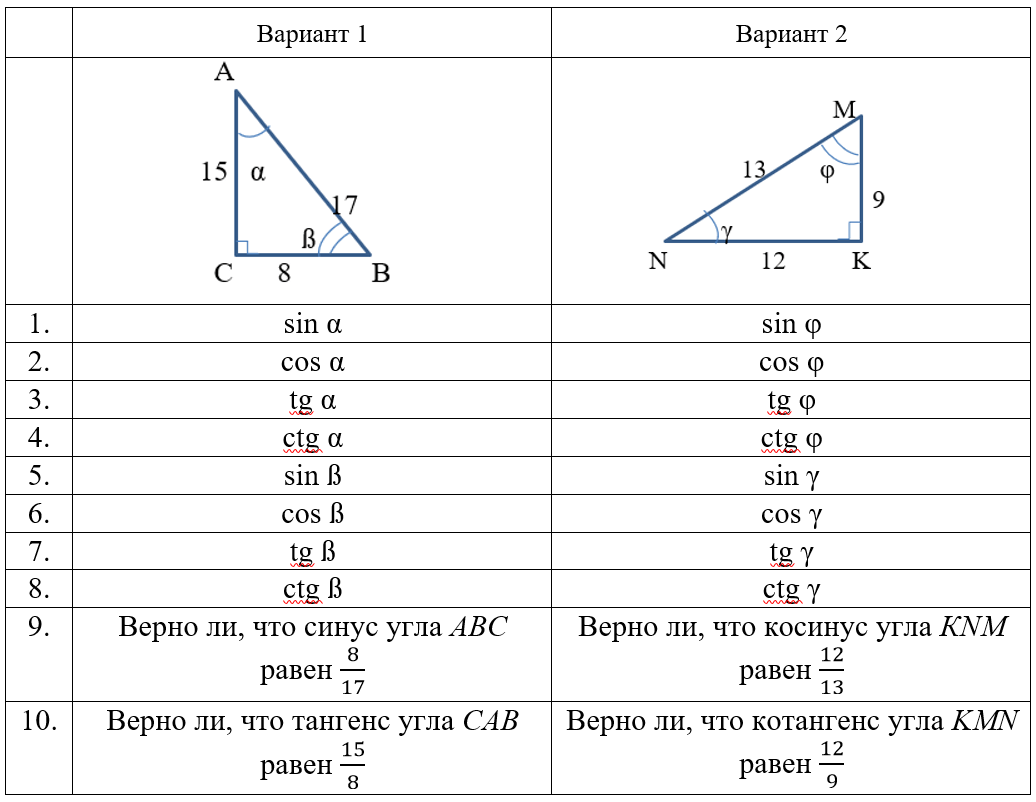
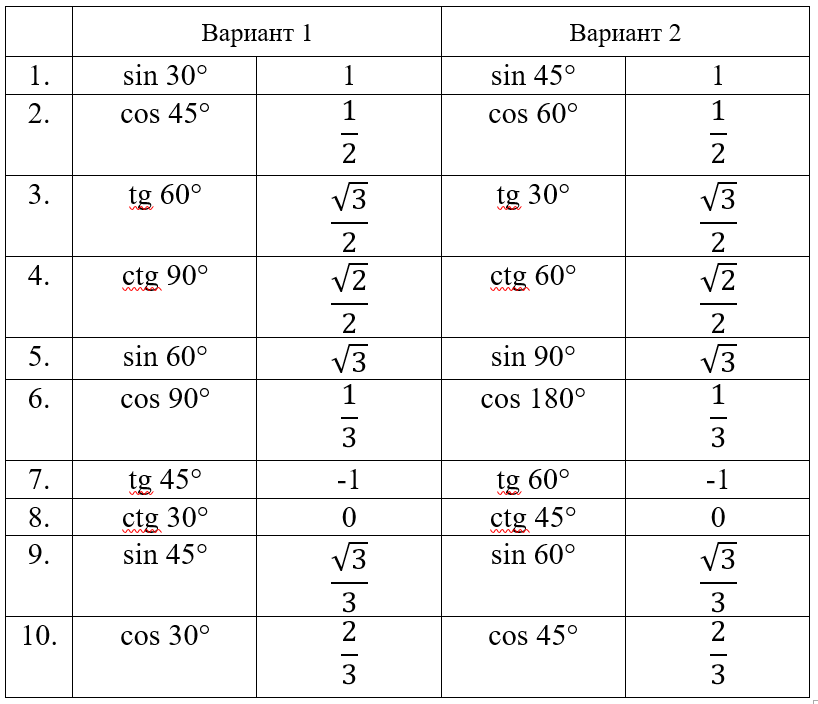
Для выполнения заданий тренажера с использованием приема «Соотнесите» учащимся предлагаем сначала выполнить свой вариант тренажера с использованием готовых таблиц для запоминания, а потом второй вариант, но уже без готовых таблиц. Таким образом, используя прием «Взаимопроверка», каждый учащийся проработает два варианта тренажера и дополнительно отработает навык нахождения ошибок, проверяя работу соседа по парте.
Рассмотрим тренажер на соотношение тригонометрических элементов и их табличных значений:
При работе с основными тригонометрическими зависимостями, предлагаем учащимся математический тренажер, в котором по известному значению нужно найти остальные тригонометрические элементы, используя основное тригонометрическое тождество и формулы зависимостей тангенса и котангенса угла от синуса и косинуса.

Отработка навыков работы с тригонометрическими формулами позволяет учащимся в дальнейшем оперировать своими умениями, «доведенными до автоматизма», при выполнении более сложных тригонометрических преобразований.



 Предложить публикацию
Предложить публикацию