Инна МАКАРЕНКО,
учитель математики
ГУО «Гимназия № 1 им. Ф.Я.Перца г. Пинска»
Цели:
— повторить решение простейших задач на проценты с помощью пропорции, научить решать более сложные задачи;
— развивать логическое мышление учащихся, умение сравнивать и анализировать;
— воспитывать научное мировоззрение, показать связь математики с другими предметами.
Решение задач
I Устные упражнения
Прочитать пропорцию и выяснить верная ли пропорция, используя основное свойство:
— Определить, является ли прямой или обратной пропорциональной зависимостью
а) возраст Забавы и длина ее волос;
б) расстояние от Киева до заставы и время, за которое Гонец доедет до Добрыни, если он движется с постоянной скоростью.
II Решение простейших задач, актуализация знаний
Задача 1
Сегодня к нам в гости прилетел Змей Горыныч. И пока он к нам летел, у него возникла проблема. Давайте поможем Змею Горынычу решить эти проблемы и сами порешаем задачи на проценты с помощью пропорции.
Итак, 1-я голова Змея Горыныча говорит: «Летел я над лесом в 300 га. И случайно сжег 25 % площади леса. Сколько га я сжег?»
Решение задачи на доске:
Всего – 300 га – 100 %
Сжёг – х га – 25 %
Решение:
Ответ: сжег 75 га
Задача 2
А вторая голова говорит: « Нет, неправильно ты все рассказала, вот как надо: Летел я над лесом. И случайно сжег 25 % площади леса. И знаю, что сжег я 75 га, а сколько всего была площадь леса?»
Решение задачи на доске:
Всего – х га– 100%
Сжег – 75 га – 25%
Решение:
Ответ: площадь леса 300 га
Задача 3
А третья голова говорит: «Летел я над лесом в 300 га. И случайно сжег 75 га леса. Сколько процентов площади я сжег?»
Решение задачи на доске:
Всего – 300 га – 100%
Сжег – 75 га – х %
Решение:
Ответ: сжег 25%
Вот и решили мы с вами все задачи Змея Горыныча. Ну вот, теперь Змей Горыныч, я думаю, все понял. Давайте посоветуем ему быть осторожным и беречь лес от пожара.
III Закрепление. Решение более сложных задач на проценты и пропорции
(Из пособия для учащихся «Математика после уроков. 6 класс», Т.С.Безлюдовой)
1) С дровяного склада в первый день отпустили 420 м³ дров, что составило 35 % имеющихся на складе. Во второй день было отпущено![]()
того, что отпустили в первый день, а остальные дрова распределили между тремя деревнями пропорционально числам 2,425; 1,125 и 0,75. Сколько кубометров дров было отпущено каждой деревне?
2) Три мальчика пошли в лес за орехами. При подсчёте собранных орехов оказалось, что число орехов у первого мальчика относилось к числу орехов второго как 3 : 4, а отношение числа орехов второго мальчика к числу орехов третьего равно 5 : 3. Сколько орехов собрал каждый, если у первого мальчика было на 102 ореха больше, чем у третьего?



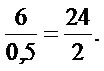


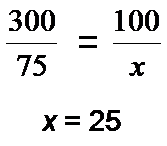

 Предложить публикацию
Предложить публикацию