Ромуальда МАХНАЧ,
ГУО «УПК Трабский ясли-сад – средняя школа»
Ивьевского района,
Гродненская область
Тема урока: Решение текстовых задач на смеси и сплавы (алгебра, 9-й класс); эффективные приемы и способы развития творческих способностей учащихся (Слайд 1).
Цель: Раскрыть возможности развития творческих способностей учащихся на уроках математики через различные методические приемы.
Задачи:
— знакомство с разнообразными приёмами и способами развития творческих способностей учащихся;
— обучение эффективным приёмам развития творческих способностей учащихся на различных этапах урока.
— изучение особенности планирования урока, направленного на развитие творческих способностей учащихся;
— создание условий для активного взаимодействия участников урока;
— развитие навыка фиксирования наблюдения (применяемые приемы, деятельность учителя и учащихся). (Слайд 2)
Ход урока
І Организационно-мотивационный этап
Здравствуйте, уважаемые коллеги!
Тема нашего урока: Решение текстовых задач на смеси и сплавы (алгебра, 9 класс); эффективные приемы и способы развития творческих способностей учащихся.
Сегодня мы вместе ответим на вопрос: какие приёмы и как часто мы используем с целью развития творческих способностей учащихся?
Надеюсь, что наша совместная работа будет плодотворной, и к концу занятия мы сможем определить разнообразные приёмы и способы развития творческих способностей учащихся на уроках математики, научимся применять их на различных этапах урока.
Прежде, чем мы приступим к занятиям, я хочу рассказать вам притчу.
«Жили-были два соседа. Пришла зимушка-зима, выпал снег. Первый сосед ранним утром вышел с лопатой убрать снег перед домом. Пока чистил дорожку, посмотрел, как там дела у соседа. А у соседа – аккуратно утоптанная дорожка (Слайд 3). На следующее утро опять выпал снег. Первый сосед встал на полчаса раньше, принялся за работу, глядит – а у соседа уже дорожка проложена. На третий день снегу намело – по колено. Встал еще раньше первый сосед, вышел наводить порядок… А у соседа – дорожка уже ровная, прямая – просто загляденье!
В тот же день встретились они на улице, поговорили о том, о сем, тут первый сосед невзначай и спрашивает:
– Послушай, сосед, а когда ты успеваешь снег перед домом убирать?
Второй сосед удивился сначала, а потом засмеялся:
– Да я его никогда не убираю, это ко мне друзья ходят!» (Слайд 4)
Итак, что вы можете сказать, о чем эта притча? (Ответы учителей)
Совершенно верно, когда есть друзья, то и трудности преодолеваются легче. Сегодня мы поработаем в группах, чтобы как можно эффективнее раскрыть возможности развития творческих способностей учащихся на уроках математики.
А чтобы в группах работать было комфортнее, предлагаю познакомиться (Слайд 5). По часовой стрелочке каждый член группы говорит комплимент своему соседу. Итак, я начинаю: Я – Ромуальда, в общении с вами я надеюсь на взаимопонимание и поддержку.
Урок для взрослых, как форма методической работы, предлагает одной части участников поставить себя на место ученика и прочувствовать на себе, как работает тот или иной прием или методика, а второй – стать наблюдателями и постараться увидеть и зафиксировать факты.
Предлагаю сформировать две группы учащихся и группу наблюдателей.
В качестве средства для наблюдения я хочу предложить вам карту наблюдения. Ваша задача – собрать информацию по созданию условий на уроке для формирования творческих способностей учащихся в соответствии с этапами урока. Ещё мне хотелось бы обратить внимание на особенность деятельности наблюдателей. Наблюдая за уроком, вы не выносите оценочное суждение и не оформляете его в виде баллов, а фиксируете факты деятельности учителя и учащихся (Приложение).
Карта наблюдения
|
Этап урока |
Формируемые творческие способности |
Средства, приемы, применяемые учителем |
Деятельность, реакция, эмоциональный отклик учащихся |
|
|
|
|
|
Немножко инструкции для «учеников»: «Пользуемся «светофором», работаем в группах или самостоятельно, учимся друг у друга.
Цели урока (для учащихся)
образовательные:
— создание условий для систематизации, обобщения и углубления знаний учащихся при решении текстовых задач на смеси и сплавы;
— повышение практической направленности предмета через решение практических задач;
воспитательные:
— формирование математической грамотности учащихся;
развивающие:
— развитие навыков логического, творческого мышления, сообразительности и наблюдательности.
ІІ Деятельностный этап – предметный урок
У древнегреческого учёного Фалеса (Слайд 6) спросили:
— Что есть больше всего на свете?
— Пространство.
— Что быстрее всего?
— Ум.
— Что мудрее всего?
— Время.
— Что приятнее всего?
— Достичь желаемого.
Я приветствую вас на уроке алгебры. Желаю вам в пространстве данного кабинета, за ограниченное время нашего урока с помощью вашего ума достичь желаемого. То есть решить все задачи стоящие перед нами (Слайд 7).
Сегодня на уроке мы займемся повторением по теме: «Решение задач на смеси и сплавы». И предлагаю начать урок с кроссворда (Слайды 8-13).
Кроссворд:
1 Частное двух чисел называют …(отношение).
2 В химии определение этого понятия звучало бы так: гомогенная смесь, образованная не менее чем двумя компонентами, один из которых называется растворителем, а другой растворимым веществом.… (раствор).
3 Сотая часть числа называется…(процент).
4 Отношение массы растворимого вещества к массе раствора называют массовой долей вещества в растворе или …(концентрация).
5 Верное равенство двух отношений называют …(пропорция).
Человеку часто приходится смешивать различные жидкости, порошки, газообразные и твердые вещества, или разбавлять что-то водой. Текстовые задачи на смеси, сплавы входят в различные сборники заданий по подготовке к итоговой аттестации по математике за курс базовой школы и включаются в варианты ЦТ.
Как вы думаете, какова цель нашего урока? (Ответы, Слайд 14)
Сегодня на уроке мы с вами повторим способы решения задач, которые связаны с понятиями «концентрация», «процентное содержание». В условиях таких задач речь идет, чаще всего, о сплавлении каких-либо металлов, растворении друг в друге различных веществ или переливании жидкостей, состоящих из нескольких компонентов.
Кто может ответить, что называется концентрацией?
Ответ: Долей (концентрацией, процентным содержанием) α основного вещества в смеси называется отношение массы основного вещества m в смеси к общей массе смеси M (Слайд 15):
Эта величина может быть выражена либо в долях единицы, либо в процентах. В большинстве случаев задачи на смеси и сплавы становятся нагляднее, если при их решении использовать схемы, рисунки, таблицы. Современные психологи утверждают, что решение одной задачи несколькими способами часто бывает более полезным, чем решение одним способом нескольких задач.
Внимание на экран. Вспомним ранее изученные способы решения задач на смеси и сплавы (Слайд 16).
1 С помощь таблицы.
2 С помощью математической модели.
3 Решение задач с помощью системы уравнений.
4 Старинный способ решения задач (Метод рыбки).
5 С помощью приравнивания площадей равновеликих фигур.
Решение задач с помощью таблицы (Слайд 17)
|
Наименование веществ, растворов, смесей, сплавов |
% содержание меди (доля содержания вещества) |
Масса раствора (смеси, сплава) |
Масса вещества |
|
|
|
|
|
Задача № 1. Имеется два сплава меди и свинца. Один сплав содержит 15 % меди, а другой 65 % меди. Сколько нужно взять каждого сплава, чтобы получилось 200 г сплава, содержащего 30 % меди?
Решение:
|
Наименование веществ, растворов, смесей, сплавов |
% содержание меди (доля содержания вещества) |
Масса раствора (смеси, сплава) |
Масса вещества |
|
Первый сплав |
15 % = 0,15 |
х г |
0,15 * х |
|
Второй сплав |
65 % = 0,65 |
(200 – х) г |
0,65 * (200 – х) = 130 – 0,65 х |
|
Получившийся сплав |
30 % = 0,3 |
200 г |
200 * 0,3 = 60 |
Сумма масс меди в двух первых сплавах равна массе меди в полученном сплаве:
Решив это уравнение, получаем х = 140. При этом значении х выражение 200 – х = 60. Это означает, что первого сплава надо взять 140 г, а второго 60 г
Ответ: 140 г, 60 г.
Решение задач с помощью математической модели (Слайд 18)
Графические иллюстрации к условию задач помогают найти правильный путь к ответу на вопрос задачи.
Изобразим каждый из растворов в виде прямоугольника, разбитого на два фрагмента (по числу составляющих элементов). Для того чтобы показать, что происходит смешивание веществ поставим знак «+» между первым и вторым прямоугольниками, а знак «=» между вторым и третьим прямоугольниками показывает, что третий раствор получен в результате смешивания первых двух. Полученная схема имеет следующий вид:
Решим задачу № 1 данным способом.
Рассматриваемый в задаче процесс можно представить в виде следующей модели-схемы:
Решение:
Пусть х г – масса первого сплава. Тогда, (200 – х) г – масса второго сплава. Дополним последнюю схему этими выражениями. Получим следующую схему:
Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):
Решив это уравнение, получаем х = 140. При этом значении х выражение 200 – х = 60. Это означает, что первого сплава надо взять140 г, а второго – 60 г.
Ответ: 140 г, 60 г.
Решение задач с помощью систем уравнений (Слайд 19)
Пусть первого сплава было x грамм, а второго y грамм. Тогда их масса равна x + y = 200, а концентрация равна 0,15x + 0,65y = 0,3 * 200. Получаем систему уравнений:
Ответ: надо взять140 г первого сплава и 60 г второго сплава.
Старинный способ решения задач или квадрат Пирсона (Слайд 20)
М1 – масса раствора с меньшей концентрацией;
a1 – меньшая концентрация раствора;
М2 – масса раствора с большей концентрацией;
a2 – большая концентрация раствора;
М1 + М2 – масса конечного раствора;
a3 – концентрация конечного раствора;
a1<a3<a2
Следует, что
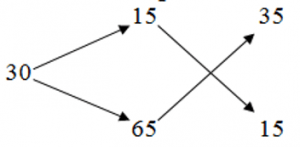
Составляем схему:
Узнаем сколько грамм сплава приходится на одну часть:
200 : (35 + 15) = 4 (грамма) – в 1 части
15 * 4 = 60 (грамм) – 2-й сплав
35 * 4 = 140 (грамм) – 1-й сплав
Ответ: надо взять140 г первого сплава и 60 г второго сплава.
Решение задач с помощью приравнивания площадей равновеликих фигур (Слайд 21)
Задача № 2. Смешали 30 %-ный раствор соляной кислоты с 10 %-ным раствором и получили 600 г. 15 %-ного раствора. Сколько граммов каждого раствора надо было взять?
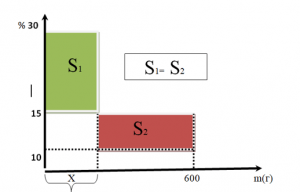
На оси х мы отмечаем массу растворов, на оси y процентное содержание растворов. Находим площади полученных прямоугольников и приравниваем их.
В данной задаче нам неизвестна масса первого вещества. Обозначим её за х г, тогда масса второго вещества равна (600 – х) г. Находим площади прямоугольников. S1 = 15x, S2 = 5(600 – x). Приравниваем эти площади. Решаем уравнение 15х = 5(600 – х). Получаем х = 150 г – масса первого раствора.
Находим массу второго раствора 600 –150 = 450 г.
Ответ: 150 г 30 %-ного раствора и 450 г 10%-ного раствора.
Зарядка для глаз
А сейчас я попрошу вас, опираясь на теоретический и практический материал, полученный во время анализа решения задач, проявить свою наблюдательность, сообразительность, творческое мышление (Слайд 22).
У меня в руках кубик. На каждой стороне кубика написано одно из заданий, которое вам нужно выполнить:
1 Опиши это… (Опиши цвет, форму, размеры или другие характеристики).
2 Сравни это… (На что это похоже? Чем отличается?)
3 Проассоциируй это… (Что это напоминает?)
4 Проанализируй это… (Как это сделано? Из чего состоит?)
5 Примени это… (Что с этим можно делать? Как это применяется?)
6 Приведи «за» и «против» (Поддержи или опровергни это).
Я бросаю кубик над каждым столом, и таким образом определяется, в каком ракурсе группа будет раскрывать понятие, которое представлено Вашему вниманию на слайде (концентрация).
Всем спасибо.
А сейчас применим все знания, которые мы возобновили, при практическом решении задач на смеси и сплавы. И я предлагаю вам сеанс одной задачи. Путём случайного выбора кубика, группы выбирают для себя способы, которыми будет решена одна и та же задача.
(Выбор способа решения задачи, по 3 варианта и решение задач в группах).
Задача (Слайд 23). Имеется два сплава меди и олова. Один сплав содержит 72 % меди, а другой 80 % меди. Сколько нужно взять каждого сплава, чтобы получилось 800 г сплава, содержащего 75 % меди?
Решение:
1-й способ
|
Наименование веществ, растворов, смесей, сплавов |
% содержание меди |
Масса раствора (смеси, сплава) |
Масса вещества |
|
Первый сплав |
72 % = 0,72 |
х г |
0,72 * х |
|
Второй сплав |
80 % = 0,8 |
(800 – х) г |
0,8 * (800 – х) = 640 – 0,8х |
|
Получившийся сплав |
75 % = 0,75 |
800 г |
800 * 0,75 = 600 |
Сумма масс меди в двух первых сплавах равна массе меди в полученном сплаве:
Решив это уравнение, получаем х = 500. При этом значении х выражение 800 – х=300. Это означает, что первого сплава надо взять 500 г, а второго 300 г
Ответ: 500 г, 300 г.
2-й способ
Пусть х г – масса первого сплава. Тогда, (800 – х) г – масса второго сплава. Дополним последнюю схему этими выражениями. Получим следующую схему:
Сумма масс меди в двух первых сплавах (то есть слева от знака равенства) равна массе меди в полученном третьем сплаве (справа от знака равенства):
Решив это уравнение, получаем х = 500 При этом значении х выражение 800 – х = 300. Это означает, что первого сплава надо взять 500 г, а второго – 300 г.
Ответ: 500 г, 300 г.
3-й способ
Пусть х г и у г – масса соответственно первого и второго сплавов, то есть пусть исходная схема имеет вид:
Легко устанавливается каждое из уравнений системы двух линейных уравнений с двумя переменными:
Решение системы приводит к результату: х = 500, y = 300. Значит, первого сплава надо взять 500 г, а второго – 300 г.
Ответ: 500 г, 300 г.
4-ий способ
Друг под другом пишутся процентные содержания меди в имеющихся сплавах, слева от них и примерно посередине – процентное содержание меди в сплаве, который должен получиться после сплавления. Соединив написанные числа черточками, получим такую схему:
Рассмотрим пары 75 и 72; 75 и 80. В каждой паре из большего числа вычтем меньшее, и результат запишем в конце соответствующей стрелочки. Получится такая схема:
Из нее делается заключение, что 72 %-ного сплава следует взять 5 частей, а 80 %-ного – 3 части (800 : (5 + 3) = 100 г приходится на одну часть.) Таким образом, для получения 800 г 75 %-ного сплава нужно взять 72%-ного сплава 100·5 = 500 г, а 80 %-ного – 100·3 = 300 г.
Ответ: 500 г, 300 г.
Интеллектуальная разминка
Давид Гильберт говорил, что тот, кто может решить следующую задачу в уме без вычислений, – тот прирождённый математик[3].
Задача (Слайд 24).
Из чашки с кофе в чашку с молоком перелили ложку кофе, затем такую же ложку смеси перелили обратно. Чего больше: молока в чашке с кофе или кофе в чашке с молоком?
Решение (первая идея).
Пусть в чашках налито по одной ложке, тогда заберем весь кофе и получим равномерную смесь. Кофе и молока будет поровну. Всегда ли будет поровну?
Поскольку перелили «туда» и обратно одну ложку, то (вторая идея) объем жидкости в чашках не изменился. Следовательно, (третья идея) сколько кофе убыло – столько молока прибыло.
Замечание. Объёмы кофе и молока в чашках могут быть неравными, можно переливать ложку туда и обратно хоть десять раз, можно плохо размешивать перелитую ложку все равно молока в кофе будет столько же, сколько кофе в молоке!
Определим случайным выбором кубика, какой вид работы ваша группа будет выполнять.
Работа с решенной задачей (Слайд 25).
1 Исследование решения:
— Сколько способов решения имеет задача?
— При каких условиях она не имела бы решения?
2 Исследование решения:
— Какие приемы наиболее целесообразны для поиска решения этой задачи?
— Возможны ли ещё какие-то другие методы решения?
3 Измените условия задачи так, чтобы задача решалась другим действием.
4 Поставьте новый вопрос к решенной задаче.
5 Поставьте все вопросы, ответы на которые еще можно найти по данному условию.
6 Измените числовые данные задачи так, чтобы появился новый способ решения или, наоборот, чтобы один из способов решения стал невозможен (работа в группах).
Итог урока (Слайд 26, 27).
У каждого из вас есть лист оценки. Прошу вас его заполнить.
|
Таблица индивидуальных достижений ФИ ________________________________________________ дата_____________________________ |
|
|
При решении задачи самым понятным для меня был метод |
|
|
При решении задачи самым интересным для меня был метод |
|
|
При решении задачи самым сложным для меня был метод |
|
|
Устная работа: |
|
|
Запись формул |
0 1 2 3 4 5 6 7 |
|
Решение задачи: |
|
|
Баллы, полученные группой |
0 1 2 3 4 5 6 7 8 9 10 |
|
Личный вклад в решение задачи (самооценка) |
0 1 2 3 4 5 6 7 8 9 10 |
|
Балл учителя |
0 1 2 3 4 5 6 7 8 9 10 |
Рефлексия (для учащихся) (Слайд 28)
Шел мудрец, а я навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал вопрос каждому. У первого спросил: «А что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил камни. У второго мудрец спросил: «А что ты делал целый день?», тот ответил: «А я добросовестно выполнил свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»
Давайте подведем итоги. И мы. Сделайте для себя вывод, кто какую работу выполнил сегодня на уроке.
Сегодня мы решили одну задачу, но при её решении разобрали разные методы решения.
А сейчас вернёмся к поставленным в начале урока целям. Какие из них вы выполнили? (ответы).
Вы успешно справились с заданиями. Мне очень приятно было с вами работать.
ІІІ Оценочно-рефлексивный этап (Слайд 29)
Урок для учащихся окончен. И я хотела бы обратиться к вам как к педагогам. Как вы считаете:
— Какие приёмы содействовали достижению целей урока?
— Какие приёмы снимали психологический дискомфорт участников?
— Какие элементы на уроке вызвали наибольший эмоциональный отклик?
— Как организовывалась учебная деятельность?
— Что дает применение этого прима?
— Как вы восприняли прием?
— Как вы отреагировали на такую технику, замечание?
— Какие виды деятельности были выполнены наиболее успешно? Назовите наиболее эффективные из них.
А теперь послушаем мнение наблюдателей. (Идёт обсуждение урока по картам наблюдения)
В завершении нашего занятия хочу предложить вам написать «Синквейн» (Слайд 30).
-
- Первая строка – слово (существительное, местоимение), обозначающее объект или предмет, о котором пойдет речь в синквейне.
- Во второй строке – два слова (прилагательные, причастия) для описания признаков и свойств выбранного объекта.
- Третья строка – три глагола, описывающие характерные действия объектом.
- Четвертая строка – фраза из четырех слов, выражающая личное отношение автора синквейна к описываемому объект.
- В пятой строке содержится одно слово, характеризующее суть объекта.
(Участники пишут синквейн)
Прочитайте, что у вас получилось.
Всем спасибо за урок. Ваша оценка очень важна для меня.
Ссылка на презентацию:
https://drive.google.com/file/d/18ZZI7xWDViZnc3EP1u5HowMnRRY7ba7S/view?usp=sharing



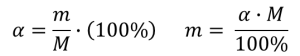


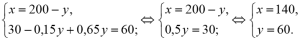


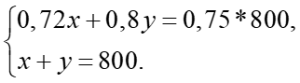

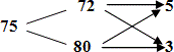

 Предложить публикацию
Предложить публикацию