Учащиеся должны самостоятельно выполнить задания на применение свойств квадратного корня. Предполагается, что к окончанию урока учащиеся будут уметь применять свойства квадратного корня в различных стандартных и изменённых условиях.
Татьяна КНЫШ,
учитель математики
ГУО «Гимназия № 1 имени Ф.Я.Перца г. Пинска»,
Брестская область
Тема: «Применение свойств квадратного корня».
Место урока в теме: 5-й урок.
Тип учебного занятия: урок применения знаний.
Цель: учащиеся должны самостоятельно выполнить задания на применение свойств квадратного корня.
Ожидаемые результаты: предполагается, что к окончанию урока учащиеся будут уметь применять свойства квадратного корня в различных стандартных и изменённых условиях.
Задачи:
образовательные – вырабатывать навыки применения свойств квадратного корня в стандартных и изменённых условиях;
развивающие – способствовать развитию логического и критического мышления, познавательного интереса, интереса к творческой деятельности, формированию навыков взаимо- и самоконтроля, функциональной грамотности;
воспитательные – воспитывать интерес к предмету; стремление к взаимопомощи, товариществу; чувство гордости за свою страну.
Оборудование: компьютер, проектор, сигнальные карточки трех цветов, раздаточный материал, презентация Power Point.
Ход урока
1 Организационный этап
– Здравствуйте, ребята! Послушайте стихотворение-загадку:
Он есть у дерева, цветка, он есть у уравнений,
И знак особый связан с ним, конечно, вне сомнений.
Заданий многих он итог, и с этим мы не спорим.
Надеемся, что каждый смог ответить: это… (корень)
2 Мотивационный этап
Проблемная ситуация
Два ученика вычисляли при n = 3 значение выражения
![]()
каждый своим способом.
Один из них рассуждал так:
![]()
при любых n.
Другой сразу подставил в алгебраическое выражение заданное значение n:
![]()
– Кто из двух верно решил задачу?
–. Найти допущенные ошибки.
– Какие знания мы здесь использовали?
Учитель подводит к формулировке темы урока. Учащиеся формулируют тему урока.
– Предлагаю отработать полученные знания, чтобы не попасть в такую ситуацию, как первый ученик.
– Открываем тетради, записываем дату, классная работа и тему урока: «Применение свойств квадратного корня».
– Девиз нашего урока: «Математику нельзя изучать, наблюдая, как это делает сосед!»
– Это слова канадско-американского математика Айвена Нивена (демонстрация фото). Он является автором доказательства иррациональности числа π, которое носит его имя, – доказательство Нивена. Я приглашаю всех к активной работе на уроке.
– Начиная любое дело, человек ставит перед собой цели. Давайте и мы определим цель сегодняшнего урока. Посмотрите на облако слов и определите цель урока.

Учащиеся формулируют цель урока.
– Цель: самостоятельно выполнить тест на применение свойств квадратного корня. А для достижения цели мы будем повторять свойства квадратного корня, применять их при преобразовании выражений.
– В конце урока за тест каждый получит отметку. А на протяжении урока вы можете копить фишки, которые будут учитываться при выставлении отметки за урок. Выполняя задания, мы будем открывать изображение события, которое произошло в Минске 14 октября 2023 года.
3 Этап проверка домашнего задания
По решениям на слайде учащиеся сверяют свои решения.
Учитель проводит опрос о правильности выполнения домашнего задания.
– Молодцы те, кто всё выполнил верно. А те, кто столкнулся с трудностями при выполнении домашнего задания, обязательно их сегодня преодолеет.
4 Этап актуализация знаний
Блицопрос (за каждый правильный ответ учащиеся получают фишку)
1) Квадратным корнем из числа а называется (число, квадрат которого равен а).
2) Арифметическим квадратным корнем из числа а называется (неотрицательное число, квадрат которого равен а).
3) Как называется знак √?
4) Сколько имеет корней уравнение, если: а > 0; а = 0; а < 0?
5) Корень из произведений неотрицательных множителей равен (произведению корней из этих множителей).
6) Как можно вынести подкоренное выражение за знак корня? (Подкоренное выражение нужно представить в виде произведения множителей и применить теорему о корне из произведения).
7) Как нужно внести множитель под знак корня? (Если множитель – неотрицательное число, множитель возводим в квадрат и вносим под корень. Если множитель – отрицательное число, преобразуем его и внесём под корень неотрицательный множитель).
8) Как избавиться от иррациональности в знаменателе дроби? (Если знаменатель дроби – корень, то числитель и знаменатель умножаем на знаменатель дроби. Если знаменатель дроби равен сумме или разности выражений, содержащих корень, то числитель и знаменатель дроби умножаем на сопряженное выражение).
Устный счёт (разминка для ума)
Приглашается ученик. С помощью указки он должен просчитать по таблице до десяти. Остальные проверяют правильность счёта. Если не ошибся, то получает фишку.
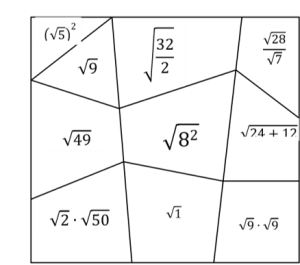
5 Этап применения знаний
Работа в парах
Найди и исправь ошибку.
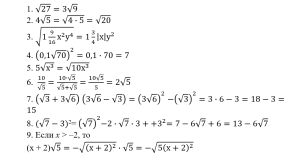
Самопроверка по слайдам. У кого все верно, получает фишку.
– Молодцы! И мне хочется сказать вам: «Пусть удача и успех всегда идут с вами рядом!»
– А вы знаете, ребята, что существует неофициальный праздник, посвященный квадратному корню? День квадратного корня – праздник, отмечаемый девять раз в столетие: в день, когда и число, и порядковый номер месяца являются квадратными корнями из двух последних цифр года.
– По объективным математическим причинам этот праздник может отмечаться строго девять раз в столетие (семь раз в первой половине века и дважды – во второй), всегда в одни и те же дни:
– 1 января ××01 года
– 2 февраля ××04 года
– 3 марта ××09 года
– 4 апреля ××16 года
– 5 мая ××25 года
– 6 июня ××36 года
– 7 июля ××49 года
– 8 августа ××64 года
– 9 сентября ××81 года
– Впервые этот праздник отмечался 9 сентября 1981 года (09-09-81). Основателем праздника является школьный учитель Рон Гордон (Ron Gordon) из города Редвуд Сити, Калифорния, США. Главным блюдом на этом «праздничном столе» обычно являются вареные кубики из овощей и выпечка в форме математического знака квадратного корня.
Физкультминутка
– Прошу всех встать. Изобразите радикал знак квадратного корня.
Учащиеся изображают радикал. Затем меняют положение на противоположное.
– Говорят, что математикам присуща дерзость ума: они не любят, когда им о чем-нибудь рассказывают, они хотят дойти до всего сами.
Устное упражнение
Площадь одного квадрата равна 24 дм2, а другого – 6 дм2. Во сколько раз сторона первого квадрата больше стороны второго? (Ответ: в 2 раза).
Один учащийся выполняет следующее задание у доски остальные в тетрадях.
Кирпич падает с высоты 1 м. С какой скоростью он упадет на землю? Во сколько раз увеличится скорость, если высота увеличится в 4, 16 раз?
Справка: Скорость свободного падения тела связана с высотой падения формулой
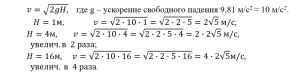
– Давайте продолжим задачу и узнаем, насколько опасно ходить под карнизами домов, ответив на вопрос:
С какой силой кирпич (сосулька) ударится о землю? Для этого проанализируем формулу:
![]() , где Δt – время взаимодействия (время удара).
, где Δt – время взаимодействия (время удара).
Из анализа формулы можно сделать вывод: чем больше Δt , тем сила удара меньше. Вот почему наличие шапки или каски на голове смягчает удар.
Энергию удара можно рассчитать: Энергия =mgH.
Пусть масса сосульки будет 3,5 кг. Посчитайте, с какой силой ударит эта сосулька, падая с высоты 6 м (например, с крыши дома).
3,5 кг ∙ 10 м/с2 ∙ 6 м = 210 кг∙м/с2 Дж.
– Мы с вами соприкоснулись с механикой удара, которая является важным элементом в физике, инженерии и спорте. Расчет силы и энергии удара может быть полезным для определения безопасности конструкций, разработки спортивного оборудования и многих других областей.
– Выполняем задания из учебника на странице 43. У доски будут работать двое учащихся (на каждый пункт), а в тетрадях учащиеся работают по вариантам (а – первый вариант, в – второй вариант).
№1.226 (а, в), 1.228 (а, в).
Если задания выполнены верно, учащиеся зарабатывают фишку.
6 Этап проверки знаний
Учащиеся получают задания для теста и бланк ответов.
Тест «Применение свойств квадратных корней»
Вариант 1

Вариант 2
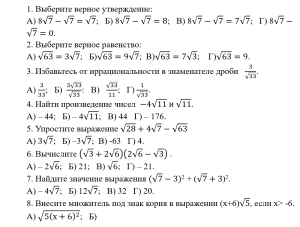
БЛАНК ОТВЕТОВ
Вариант____ ФИО_________________________________________________________________
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Вариант ответа |
|
|
|
|
|
|
|
|
|
|
После выполнения учащиеся обмениваются бланками ответов и проводят взаимопроверку ответов по слайду.
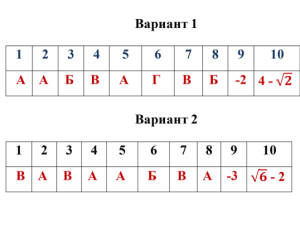
Учащиеся выставляют отметки за тест.
– Вот мы и открыли изображение события, которое произошло в Минске 14 октября 2023 года. Как вы думаете, о каком событии идёт речь?

14 октября 2023 года в индустриальном парке прошло «ТракторШОУ». Поводом для проведения мероприятия выбрана знаменательная дата – 70-летие белорусского тракторостроения. 14 октября 1953 года с конвейера Минского тракторного завода сошел первый серийный трактор полностью белорусского производства от конструкторской разработки до готовой машины. За эти годы в каталоге отечественной техники появилось больше сотни моделей. На любой вкус. От крупногабаритных самосвалов до трактора-беспилотника. В масштабном мероприятии приняло участие восемь команд из шести областей, Белорусской сельхозакадемии и БГАТУ. Победители состязаний получили тракторы» BELARUS». Также в программу шоу вошла выставка ретро-тракторов, силовое шоу, катание на тракторах и концерт. Этим мероприятием сказали спасибо людям, которые работают на белорусских тракторах, обеспечивая продовольственную безопасность нашей страны. И, конечно, отпраздновали такую замечательную дату – 70-летие отечественного тракторостроения, — которая важна не только для Минского тракторного завода, но и для нашей промышленности в целом. Ведь белорусские тракторы – настоящий повод для гордости!
7 Этап подведения итогов. Информация о домашнем задании, инструктаж по его выполнению
– Откройте дневники, запишем домашнее задание: повторить § 5, выполнить письменно № 1.268, № 1.245 №1.282(а, б); по желанию – №1.271.
– Сегодня мы повторили свойства квадратного корня, применяли их при преобразовании выражений, проверили уровень усвоения темы. Выполняя разнообразные задания, вы иногда допускали ошибки. Важно вовремя найти и исправить эти ошибки, понять, почему они появились, и стараться впредь не допускать их.
– Достигли ли поставленной цели?
– Каждый из вас сегодня получит отметку. Я прошу вас самим оценить свою работу на уроке.
Приём «Светофор»
– Было трудно, не всё смог выполнить – красный.
– Почти со всем справился сам, но есть над чем поработать – жёлтый.
– У меня всё получилось, я всё понял – зелёный.
– Спасибо за урок. Мне было приятно с вами поработать.




 Предложить публикацию
Предложить публикацию