Алла МЕНЬКО,
учитель математики
ГУО «Гимназия № 1 г. Новогрудка»,
Гродненская область
Дидактическая цель урока: к концу урока учащиеся будут владеть материалом по теме на репродуктивном уровне.
Создать условия для формирования:
– ценностной компетенции посредством бесед о рационализме и экономии;
– социальной компетенции через обсуждение роли путешественника;
– компетенции самоопределения посредством определения личностно значимой цели, осуществления рефлексии и самооценки;
– учебно-познавательной компетенции через необходимость определять и соблюдать последовательность действий по достижению целей;
– математической компетенции через необходимость применения различных приёмов мыслительной деятельности в процессе работы с материалом урока.
Прогнозируемый результат:
– закрепление умений и навыков решения рациональных неравенств;
– формирование умения планировать свою работу;
– достижение каждым учащимся того уровня умений и навыков, который ему необходим.
Тип урока: закрепления и совершенствования знаний и умений.
Формы работы с учащимися: фронтальная, индивидуальная, коллективная, с использованием ЭОР.
Методы и технологии, используемые на уроке: проблемно-поисковые, ИКТ, дифференцированные.
Оборудование: интерактивная доска, учебник.
Дидактические средства: рабочая тетрадь, раздаточный материал.
Ход урока
I Организационный момент
Здравствуйте ребята. Я рада поприветствовать вас на сегодняшнем уроке и хочу пожелать вам хорошего настроения и продуктивной работы.
II Проверка домашнего задания
Для начала мы проверим домашнее задание. На экране можете увидеть правильные ответы к номерам. Сравните их со своими ответами.
ІІІ Определение темы урока
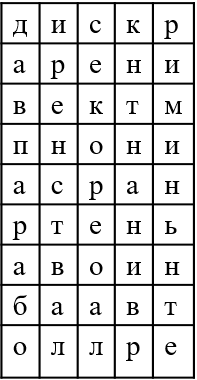 Разгадайте головоломку. В путанице букв найдите ответы на вопросы.
Разгадайте головоломку. В путанице букв найдите ответы на вопросы.
1) Число, влияющее на количество корней квадратного трехчлена.
2) График квадратичной функции.
3) Число, обращающее уравнение в верное равенство.
4) Числовой промежуток, состоящий из множества чисел, находящихся между двумя данными числами, не включая их.
Определение темы и постановка целей урока (учащиеся сами определяют тему урока и цели).
Запишите в тетрадях число, классная работа.
IV Актуализация опорных знаний и умений
Прежде чем приступить к основному этапу урока, сначала повторим алгоритм решения дробно-рациональных неравенств и их систем.
Учащиеся называют этапы решения
1 Решение рационального и дробно-рационального неравенства. Метод интервалов
1) Привести неравенство к виду
2) Найти ОДЗ (для дробно-рационального неравенства).
3) Найти нули.
4) Отметить найденные нули с учетом ОДЗ на оси Ох.
5) Определить знак на каждом интервале.
6) Включить необходимые промежутки в ответ.
2 Решение системы неравенств
1) Решить первое неравенство.
2) Решить второе неравенство.
3) Найти пересечение числовых множеств, полученных в пунктах 1 и 2.
Повторим на примере алгоритм решения рационального неравенства методом интервалов.
1. В каждом множителе коэффициент при старшей степени переменной должен быть положительный, для этого надо вынести минус из всех множителей, в которых коэффициент при старшей степени отрицательный, и если перед выражением все же остался знак минус, то надо все неравенство умножить на (-1).
2. Решить уравнение
3. На числовой прямой отложим все полученные значения и проведем кривую знаков.
4. Выпишем ответ для знака сравнения ≤:
![]() Реши самостоятельно. Учащиеся выполняют взаимопроверку.
Реши самостоятельно. Учащиеся выполняют взаимопроверку.
(2х-5)(х+3)≥0; (5х-2)(х+4)<0
V Практическое применение знаний
Решение заданий из учебника. (По одному учащемуся на каждый пример вызываются к доске, остальные работают в тетрадях. За каждое правильное решение ставится по одному баллу на полях карандашом).
№ 3.177 (а, в), 3.179 (а, в)
VI Физкультминутка
VII Контроль усвоения материала (самостоятельная работа)
Проверку выполняют самостоятельно, выставляя баллы на полях.
|
I вариант |
II вариант |
|
1. Определите нули левой части неравенства 2 (х – 5) (2х + 1) > 0. |
1. Определите нули левой части |
|
2.Решите неравенство |
2. Решите неравенство |
|
3. Найдите число целых положительных решений неравенства |
3. Найдите разность между |
VIII Подведение итогов
– Какую цель мы ставили в начале урока?
– Наша цель достигнута?
– Что нам помогло справиться с затруднениями?
– Какие знания нам пригодились при выполнении заданий на уроке?
– Всё ли получилось?
В ходе урока учащиеся закрепили умение решать рациональные неравенства, рассмотрели решение рациональных неравенств различного уровня сложности. Учащиеся на практике показали умение применять метод интервалов при решении рациональных неравенств. Особое внимание следует уделить решению нестрогих рациональных неравенств.
IX Домашнее задание
Учебник № 3.204, 3.205
III уровень № 3.204 (а), 3.205 (а);
IV уровень № 3.204 (а, б), 3.205 (а, б);
V уровень № 3.204 (в, г), 3.205 (в, г).
Сборник экзаменационных материалов
III уровень Вариант 23 № 5, Вариант 24 № 5;
IV уровень Вариант 3 № 7, Вариант 67 № 8;
V уровень Вариант 63 № 10, Вариант 65 № 10.



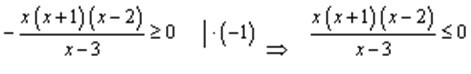
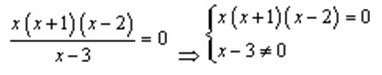


 Предложить публикацию
Предложить публикацию