В материале представлен опыт по практико-ориентированным задачам учителя математики В.Н.Гончарова, участника заключительного этапа республиканского конкурса профессионального мастерства «Учитель года Республики Беларусь – 2020».
 Владимир ГОНЧАРОВ,
Владимир ГОНЧАРОВ,
учитель математики
ГУО «Залесская средняя школа» Чечерского района,
Гомельская область
Использование практико-ориентированных задач позволяет учителю организовать деятельность учащихся, отвечающую новым образовательным задачам. Из собственного опыта отмечу, что учителям следует делать более выраженный акцент на практико-ориентированные задачи. Кроме того, педагоги могут использовать свой творческий потенциал для конструирования задач, отвечающих актуализации жизненного опыта учащихся, их интеллектуально-психологического потенциала в образовательных целях, так как навыки решения практико-ориентированных задач позволят, в определенной степени, решать проблему формирования функциональной грамотности учащихся и будут способствовать повышению качества предметных компетенций
Важным методическим моментом в плане качественного обучения учащихся навыкам решения практико-ориентированных задач является умение учителя распределить задачи по уровням сложности и содержательным линиям.
Уровни сложности практико-ориентированных задач
I уровень – задачи, в которых проведено сопоставление «реальный объект – математическая модель».
Пример: кабина автомобиля «МАЗ», имеет форму прямоугольного параллелепипеда, площадь нижней грани которого равна 1,8 м2. Вычислите объем кабины, если ее высота равна 1,5 м.
II уровень – задачи, в которых нет прямого указания на математическую модель, но реальные объекты и взаимоотношения между ними можно однозначно сопоставить с математическими объектами и операциями.
Пример: определите длину лестницы, прислоненной к дереву, если верхний конец лестницы касается дерева на высоте 4 м, а нижний конец лестницы находится на расстоянии 3 м от дерева.
III уровень – задачи, в которых реальные объекты и отношения задачи неоднозначно соотносимы с математическими объектами, и здесь требуется учесть реально сложившиеся условия, которые влияют на выбор соответствующей ей математической модели.
Пример: постройте чертеж и определите самый короткий путь, по которому можно добраться из г. Калинковичи в г. Слуцк железнодорожным транспортом.
IV уровень – задачи, которые в явной форме не выделяют объекты и отношения между ними, а их математические эквиваленты могут быть неизвестны школьникам.
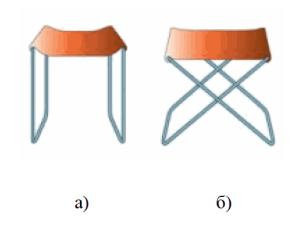
Пример: определите, на какой табурет – а или б – можно сесть без риска оказаться на полу?
Содержательные линии практико-ориентированных задач могут иметь применение на уроках в течение как одной, так и нескольких тем. В своей практической деятельности я чаще провожу распределение задач по содержательным линиям и включаю туда как задачи одного уровня сложности, так и задачи различных уровней сложности. В качестве примера приведу несколько задач содержательной линии «Прямоугольный треугольник»:
1) Какова длина лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м?
2) Пожарным требуется развернуть лестницу. Длина лестницы 10 м. Определите на какой высоте находится окно дома, если нижний конец лестницы находится на расстоянии 8 м. от стены дома.
3) Для замены лампочки, висящей на высоте h, воспользуйтесь лестницей длиной m. При каких условиях можно заменить лампочку, если лестница образовывает с опорой угол α.
Задачи этой содержательной линии я применяю как в различных темах («Теорема Пифагора. Теорема, обратная теореме Пифагора», «Соотношения между элементами прямоугольного треугольника»), так и в разных классах (VIII и IX классы). При изучении темы «Теорема Пифагора. Теорема, обратная теореме Пифагора» в качестве одного из заданий предлагаю учащимся соотнести, какая из вышеизложенных задач, 1 или 2, соответствует теореме Пифагора, а какая соответствует обратной теореме.
Содержательные линии практико-ориентированных задач могут включать задачи как целого раздела, так и определенной темы в разделе. К примеру, можно взять задачи, относящиеся к разделу «Четырехугольники», или сузить до темы «Трапеция».
Выделю еще один важный аспект: процесс применения задач практико-ориентированного характера в моей практической деятельности носит системный характер и неразрывно проходит через все темы геометрического материала, изучаемого в школьном курсе математики.
Практико-ориентированные задачи используются мной на различных этапах урока. На этапе актуализации они выступают как средство повторения ранее изученного материала и подготавливают учащихся к восприятию нового материала.
Например, на уроке геометрии в 8-м классе при обобщении материала по теме «Площади многоугольников», создаю производственную ситуацию, в которой учащиеся, поставив себя на место рабочего, смогут увидеть и оценить значение математических знаний. Примером такой ситуации может служить задача, в которой необходимо произвести настил паркетного пола заданного размера. При этом паркетные плитки будут иметь форму прямоугольного треугольника параллелограмма и равнобедренной трапеции. Учащимся требуется выполнить один из вариантов настила и посчитать, сколько плиток каждого вида потребуется.
Во время этапа изучения нового материала использую задачи практической направленности как элемент исследования, для вывода определений геометрических понятий, теорем, связанных с ними. (Приложение 1)
На этапе закрепления знаний практико-ориентированные задачи служат для выработки умений оперировать полученными знаниями. Пример. Кабинет математики имеет форму прямоугольного параллелепипеда. Сколько потребуется желтой краски, чтобы покрасить стены кабинета, имеющего размеры 8,5 м, 6,5 м, 3 м, если на 1 м2 расходуется 150 граммов краски.
Также считаю необходимым предлагать учащимся в качестве домашнего задания самим составлять практико-ориентированные задачи.
На заключительном этапе урока – выступают в роли индикаторов для оценки знаний учащихся.
Практико-ориентированные задачи могут выступать не только как элементы урока, но и перерастать во весь урок для организации групповой работы учащихся по выработке умений строить с помощью математики различные модели, несложные реальные процессы и исследовать их.
Для более качественного контроля и оценки знаний учащихся практико-ориентированные задачи геометрического характера я включаю в состав контрольных работ.
Активное использование практико-ориентированных задач геометрического характера в образовательном процессе доказывает свою эффективность не только в формировании навыков решения геометрических задач, но и является эффективным средством формирования функциональной грамотности учащихся. Такая работа позволяет учащимся добиваться успехов в различных конкурсах, где требуются умения решать задачи прикладного характера: КВИЗ «Почувствуй себя инженером!», олимпиада по направлению «Логистика», «Бизнес-энкаунтер», конкурс «Школьных бизнес-компаний».
Приложение 1
Фрагмент урока (создание проблемной ситуации) с применением задачи практико-ориентированного характера
Тема: Подобные треугольники.
Класс: VIII.
Тип урока: урок изучения и первичного закрепления новых знаний.
Цель урока:
– создание условий для формирования представлений учащихся о подобных треугольниках, признаках подобия треугольников, для развития умений учащихся использовать их при решении геометрических задач.
Задачи:
– обеспечить актуализацию субъективного опыта учащихся;
– создать условия для изучения нового материала используя анализ и обобщения;
– способствовать деятельности учащихся по первичному закреплению ими полученных знаний;
– обеспечить ситуации, способствующие развитию аналитического мышления;
– продолжить работу по развитию логического мышления.
Ход урока
Создание проблемной ситуации
Притча: «Усталый, пришел северный чужеземец в страну Великого Хапи. Солнце уже садилось, когда он подошел к великолепному дворцу фараона, что-то казал слугам. Те мгновенно распахнули перед ним двери и провели его в приемную залу. И вот он стоит в запыленном походном плаще, а перед ним на золоченном троне сидит фараон. Рядом стоят высокомерные жрецы, хранители вечных тайн природы.
– Кто ты? – спросил верховный жрец?
– Зовут меня Фалес. Родом я из Милета.
Жрец надменно продолжал:
– Так это ты похвалялся, что сможешь измерить высоту пирамиды, не взбираясь на нее? – жрецы согнулись от хохота. – Будет хорошо, – насмешливо продолжал жрец, – если ты ошибешься не более чем на сто локтей.
– Я могу измерить высоту пирамиды и ошибусь не более чем на пол-локтя. Я сделаю это завтра.
Лица жрецов потемнели. Какая наглость! Этот чужестранец утверждает, что может вычислить то, чего не могут они – жрецы Великого Египта.
– Хорошо, сказал фараон. – Около дворца стоит пирамида, мы знаем ее высоту. Завтра проверим твое искусство».
Ребята, а кто-нибудь из вас знает, как Фалес Милетский измерил высоту пирамиды? (Проблемная ситуация на уроке, основанная на практико-ориентированной задаче)




 Предложить публикацию
Предложить публикацию