Развитие читательской грамотности учащихся на уроках математики. Авторские тренажеры и приемы работы с ними

Татьяна ТУРОВЕЦ,
учитель математики
ГУО «Средняя школа № 9 г. Мозыря»,
Гомельская область

Одна из важнейших задач современного образования – формирование функциональной грамотности учащихся. Под функциональной грамотностью мы понимаем способность человека вступать в отношения с внешней средой, быстро адаптироваться и функционировать в ней. Основы функциональной грамотности закладываются в начальной школе, в среднем звене продолжается ее активное развитие путем внедрения различных приемов в учебный процесс.

Особое место среди метапредметных компетенций занимает работа с информацией и ее анализ. Эффективное обучение в школе невозможно без сформированности у учащихся читательской грамотности. В исследовании РISA (Международная программа по оценке образовательных достижений учащихся) так раскрыто это понятие: «Читательская грамотность сегодня – это способность человека понимать и использовать письменные тексты, размышлять о них и заниматься чтением для того, чтобы достигать своих целей, расширять свои знания и возможности, участвовать в социальной жизни».

Рассмотрим математический тренажер по теме «Тригонометрические формулы» на уроках геометрии в 9-м классе и его использование для развития читательской грамотности учащихся.

Тригонометрические формулы (тренажер)

Тренажер в готовом виде целесообразно использовать для развития вычислительных навыков учащихся, но если речь идет о развитии читательской грамотности, то задача учителя – научить ребят работать с информацией и анализировать ее.

Предлагаю использовать такие приемы. Например, во втором задании для нахождения неизвестного элемента основного тригонометрического тождества можно использовать прием «Потерянный элемент». При использовании этого приема предлагаем тождества, записанные в готовом виде, а после – тождества со вставленными в них известными элементами. Учащимся необходимо проанализировать алгоритм выражения одного элемента через другой. После того как алгоритм отработан, предлагаем решить задачу наоборот, исходя из того, что заданный первый элемент нам неизвестен. Таким образом, алгоритм выражения будет отработан в разных порядках и формулы будут запоминаться легче.

Рассмотрим тренажер «Задания для любознательных», который возможно применить на уроках алгебры в 9-м классе и при подготовке к выпускным экзаменам.

Найдите значение выражения:

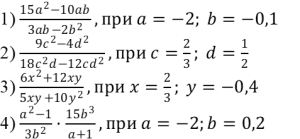
Для того чтобы научить учащихся видеть формулы сокращенного умножения и элементы, которые можно вынести за скобки, грамотно анализировать предложенные выражения, предлагаю прием «Лови ошибку». При использовании этого приема предлагается решение первого задания с заведомо допущенной одной или несколькими ошибками как на начальных преобразованиях, так и при последующем применении формул. Остальные задания выполняются с учетом исправленных ошибок в первом задании.

Стоит отметить, что прием можно использовать и в другом варианте. Например, предлагаем учащимся формулы, подходящие для выполнения данных преобразований, с заведомо допущенными ошибками, которые необходимо исправить, а после совместно с учениками разрабатываем алгоритм выполнения преобразований.

Прием «Составь алгоритм». На доске записан пример и его решение. С помощью учителя учащиеся анализируют готовое решение и составляют алгоритм, который применяют при решении остальных заданий. Вводится система рассуждений, анализ решения, учащиеся учатся работать над схематической записью числовых выражений, изучают систему рассуждений, отрабатывают математические правила. В качестве контроля и коррекции знаний можно предложить самостоятельно разработать алгоритм решения по заранее заготовленным заданиям. Прием может быть реализован на любых учебных предметах в качестве работы с текстовой информацией – трансформируется в прием «составь план», тем самым позволяя учителю развивать читательскую грамотность учащихся.

При подготовке к выпускным экзаменам не стоит забывать о работе со справочными материалами. Так, на уроках геометрии в 9-м классе целесообразно использовать прием «Корзина идей» на уроках объяснения и первичного закрепления изученного материала. На начальном этапе урока, когда происходит процесс актуализации знаний по теме, учащимся предлагается  записать все, что имеет отношение к заявленной теме, происходит обобщение накопленного опыта и подготовка к восприятию нового материала.

Алгоритм работы с приемом «Корзиной идей»:

– объявляется тема урока;
– индивидуальная работа – каждый ученик тезисно записывает в тетради все, что ему известно по теме; этап длится недолго – 2–3 минуты;
– работа в парах или в группах – учащиеся обмениваются информацией, выясняя, в чем совпали их мнения, а в чем возникли разногласия; время проведения – 3 минуты;
– работа с классом – на этом этапе каждая группа высказывает свое мнение по теме, приводит свои знания или высказывает идеи по данному вопросу, причем ответы не должны повторяться; все высказывания учитель кратко записывает на доске.

В «корзину» сбрасывается все, что имеет отношение к теме урока: идеи, формулы, факты, предположения, термины, понятия и определения.

Рассмотрим математический тренажер по геометрии по теме «Правильные многоугольники» и вариант его применения с приемом «Взаимная проверка».

Правильные многоугольники (тренажер)

«Взаимная проверка». Прием, направленный на воспитание чувства ответственности при проверке заданий, выполненных другими учащимися, развитие внимания, читательской грамотности. При проверке письменного домашнего задания, самостоятельной работы по математике можно предложить ученикам обменяться тетрадями с соседом по парте, проверить выполнение заданий, поставить оценку и рассказать о допущенных ошибках, обсудив спорные вопросы. Правильные ответы называются учителем, учащиеся сравнивают ответы и находят ошибку в случае необходимости.    

Поделиться ссылкой: