Першы ўрок геаметрыі па тэме “Уласцівасці паралельных прамых. Уласцівасці вуглоў, утвораных пры перасячэнні дзвюх паралельных прамых сякучай”.
Марына ІГНАЦІК,
настаўнік матэматыкі
ДУА “Дварэцкая сярэдняя школа”
Дзятлаўскага раёна,
Гродзенская вобласць
Мэта:
– адукацыйная: стварыць умовы для ўстанаўлення сувязі паміж прыметамі і ўласцівасцямі паралельных прамых; засваення ўласцівасцей паралельных прамых з апорай на іх прыметы; выпрацоўкі навыкаў прымянення ўласцівасцей паралельных прамых і вуглоў, утвораных пры перасячэнні дзвюх паралельных прамых сякучай да рашэння задач на доказ і вылічэнне;
– развіваючая: стварыць умовы для развіцця лагічнага і матэматычнага мыслення, пазнаваўчай актыўнасці вучняў, вуснага і пісьмовага маўлення вучняў, уменняў рабіць высновы і абагульненні;
– выхаваўчая: стварыць умовы для выхавання асобы, здольнай да развіцця і супрацоўніцтва, здольнай самастойна прымаць рашэнні і аргументавана адстойваць свае перакананні, адчуваць адказнасць за выніковасць работы.
Ход урока
I Арганізацыя занятку. Праверка дамашняга задання
Узаемаправерка правільнасці рашэння дамашніх задач, фармулёвак прымет паралельных прамых. Узаемаацэнка. Абмеркаванне пытання.
II Актуалізацыя апорных ведаў. Пастаноўка задач
– У Старажытнай Грэцыі ўсіх аратараў вучылі геаметрыі, паколькі геаметрыя вучыць разважаць і даказваць. Гаворка чалавека, які валодае здольнасцю аргументавана даказваць свае высновы, успрымаецца найбольш пераканаўча.
Старажытнагрэчаскі філосаф і матэматык Фалес (640/624 – 548/545 да н. э.) (дэманстрацыя партрэта) першым пачаў “гульню” пад назвай “Дакажы”, якая працягваецца ўжо два з паловай тысячагоддзі. Напрыклад, егіпцяне, перадаючы веды вучню, казалі: “…рабі, як робіцца”. А Фалес ставіў пытанне “Чаму гэта так?” і стаў не толькі назіраць розныя ўласцівасці геаметрычных фігур, але і выводзіць адны ўласцівасці з другіх.
– Скажыце, калі ласка, пры вывучэнні якой тэмы мы з вамі таксама гэта спрабавалі рабіць? (Адказы вучняў)
– Правільна, пры вывучэнні тэарэм аб прыметах і ўласцівасцях раўнабедранага трохвугольніка.
На слайдах дэманструюцца апорныя канспекты для паўтарэння паняццяў: умова і заключэнне тэарэмы, прамая і адваротная тэарэма.
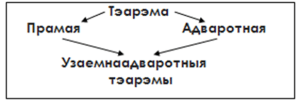
– Давайце паспрабуем сфармуляваць нашыя вучэбныя задачы на сённяшні ўрок. (Адказы вучняў)
III Вывучэнне новага матэрыялуВучням прапаноўваецца раздатачны матэрыял з фармулёўкамі прымет паралельных прамых і на дошцы дэманструецца табліца.
| Прымета 1 | Прымета 2 | Прымета 3 |
| Умова | Умова | Умова |
| Заключэнне | Заключэнне | Заключэнне |
Вучням неабходна разрэзаць фармулёўкі прымет паралельных прамых, раздзяліўшы іх на ўмовы і заключэнні, а затым запоўніць атрыманымі карткамі прапанаваную табліцу з дапамогай магнітаў. (Работа ў парах).
– Што нам неабходна цяпер зрабіць, каб візуальна ўбачыць фармулёўкі ўласцівасцей паралельных прамых? (Памяняць месцамі ўмовы і заключэнні.)
Дэманструецца адпаведны слайд, вучні фармулююць уласцівасці паралельных прамых.
– Дык як звязаны прыметы і ўласцівасці паралельных прамых? (Прыметы і ўласцівасці паралельных прамых узаемна адваротныя.)
– Давайце праверым, ці верныя тэарэмы, адваротныя прыметам паралельнасці прамых: “Тэарэмы аб вуглах, утвораных дзвюма паралельнымі прамымі і сякучай”.
У дапамогу вучням дэманструецца слайд для доказу тэарэм па гатовых чарцяжах і прапаноўваецца магчымасць работы з падручнікам с. 99.
– Якім метадам будзем карыстацца пры доказе першай уласцівасці? У чым заключаецца сутнасць гэтага метаду? (Дэманструецца апорны канспект).
|
Дадзена: |
Дадзена: |
Дадзена: |
 |
||
|
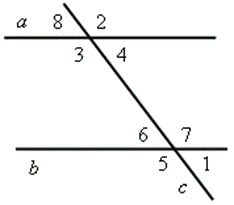Даказаць: |
Даказаць: |
Даказаць: |
IV Замацаванне вывучанага. Рашэнне задач
1. Вусная работа (франтальная работа, прымаюцца адказы з кароткім аргументаваннем) (заданні І, ІІ узроўню):
1) тэст 1, 2 (тэарэтычнае заданне, падручнік, с. 100);
2) № 145 па гатовых чарцяжах (практычнае заданне, падручнік, с. 101).
(Адказы: 125°; 118°; 38°; 97°).
2. Пісьмовае выкананне задач па гатовых чарцяжах каля дошкі (тры вучні) з афармленнем рашэння і наступным вусным кароткім тлумачэннем перад класам (раздатачны матэрыял, заданні ІІІ узроўню).
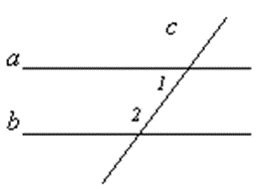
а || b, сякучая с
1) ∠2 = 3 ∙∠1. Знайсці большы вугал. (Адказ: 135°)
2) ∠1 = ∠2 – 30°. Знайсці ∠1, ∠2. (Адказ: 75°; 105°)
3) ∠2 : ∠1 = 3 : 2. Знайдзіце меншы вугал. (Адказ: 72°)
Асобныя вучні выконваюць індывідуальнае заданне ў рамках падрыхтоўкі да алімпіяды (картка, заданне V узроўню).
3. Пісьмовае выкананне задач каля дошкі і на месцах (заданні ІV узроўню):
1) на вылічэнне № 148 (падручнік, с. 102). (Матэрыял для паўтарэння: бісектрыса вугла, раўнабедраны трохвугольнік, прымета раўнабедранага трохвугольніка). (Адказ: 50 см)
2) на доказ і вылічэнне № 149 (падручнік, с. 102). (Матэрыял для паўтарэння: прыметы роўнасці трохвугольнікаў). (Адказ: 4 см)
4. Таму, хто спраўляецца з заданнямі ІV узроўню, прапануецца для выканання заданне на доказ, № 162* (на 9–10 балаў).
V Тлумачэнне дамашняга задання
§ 17, № 146, № 147.
VI Рэфлексія
Састаўленне на дошцы калажу з гексаў (шасцівугольнікаў) “Вуглы, утвораныя пры перасячэнні дзвюх паралельных прамых і сякучай”. (Групавая работа).
Заўвага. Вучні атрымліваюць адзін гекс з надпісам і дзевяць пустых гексаў, якія яны павінны дапоўніць неабходнымі надпісамі.
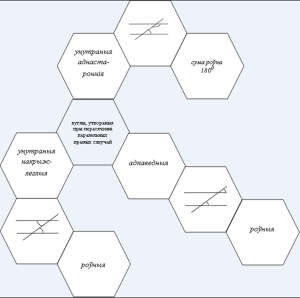
VII Падвядзенне вынікаў
Самаацэнка і ўзаемаацэнка вучняў (у дапамогу дэманструецца слайд з апорай на якасць выканання вучэбных задач да ўрока і асноўныя патрабаванні да вучэбнай дзейнасці вучняў згодна вучэбнай праграме).
– Правільна ўжываю тэрміны і выкарыстоўваю паняцці:… (прамая і адваротная тэарэма, прымета і ўласцівасць, метад ад адваротнага).
– Ведаю … (прыметы паралельнасці і ўласцівасці паралельных прамых).
– Адрозніваю і правільна вызначаю… (накрыжлеглыя, адпаведныя і аднастароннія вуглы пры дзвюх прамых і сякучай).
– Умею даказваць … (прыметы паралельнасці і ўласцівасці паралельных прамых).
– Умею рашаць геаметрычныя задачы на доказ і вылічэнне, прымяняючы… (прыметы паралельнасці і ўласцівасці паралельных прамых).
Ацэньванне вучняў.
Предложить публикацию