Повторение и закрепление определения корня n-й степени из числа, свойства корней n-й степени из числа и применение их при решении заданий разного типа и разного уровня сложности.
Валентина ЛАВРУЩИК,
учитель математики
ГУО «Средняя школа № 1 г. Новогрудка»,
Гродненская область
Задачи:
– повторить и закрепить определение корня n-й степени из числа, свойства корней n-й степени из числа и применять их при решении заданий разного типа и разного уровня сложности;
– развивать вычислительные навыки и умения, логическое мышление;
– воспитывать ответственность, самостоятельность учащихся.
Оборудование: мультиборд, , карточки с заданиями для групповой работы, мобильные телефоны, презентация (https://docs.google.com/presentation/d/1_YttEiiSpRYX3dXqlmHJLfQ5NX8SRGke/edit?usp=share_link&ouid=110077429701320128892&rtpof=true&sd=true).
Ход урока
1 Организационный момент
Приветствие, налаживание эмоционального контакта, ознакомление с темой учебного занятия, определение целей и постановка задач совместно с обучающимися.
Прием целеполагания «Волшебная корзина»
Учащиеся знакомятся с темой урока (Слайд 1), ставят перед собой задачи, записывая их на листочках и складывают в корзину.
2 Актуализация знаний
Прием «Проблемный вопрос»
– Что называется корнем n-й степени из числа?
– Что называется арифметическим корнем n-й степени из числа?
– Всегда ли можно извлечь корень n-й степени из числа?
– Корень какой степени из отрицательного числа не существует?
Прием «Логическая цепочка» (Слайд 2)
Учащиеся по цепочке выполняют вычисления.
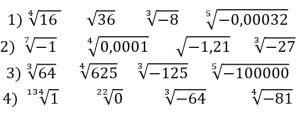
Прием «Верно – не верно» (Слайд 3)
1) -2 является арифметическим корнем четвертой степени из числа 16?
2) -0,5 является корнем четвертой степени из числа 0,0625?
3) -5 является корнем кубическим из числа -125?
4) -3 является корнем кубическим из числа 27?
3 Практическая часть
Прием «Кто быстрее?»
Учащиеся на листочках стрелками соединяют выражения левой части с выражениями правой части таким образом, чтобы получились формулы, выражающие свойства корня n-й степени. Один учащийся выполняет это задание на мультиборде (Слайд 4).
После выполнения проверяется правильность получившихся формул.
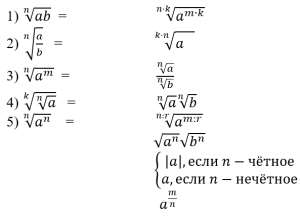
Электронная версия: https://learningapps.org/watch?v=psdm4yzjt23.
Работа в группах
Учащиеся делятся на группы (по уровню обучаемости). Каждая группа получает свое задание. Ребята в группах обсуждают ход решения, вырабатывают тактику и распределяют роли. После окончания работы проверяется правильность выполнения.
Группа 1
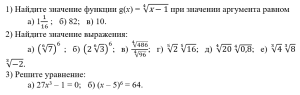
Группа 2
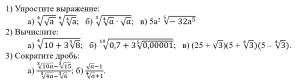
Группа 3
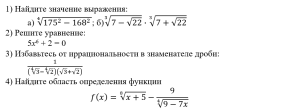
Ответы к заданиям на слайде 5.
Физкультминутка
Учащиеся получают задание: найти свой ответ (ответы размещены по классу в разных местах) к выполнению действий.

Выполнение Google-теста (Слайд 6)

После выполнения теста учащиеся вводят ответы, на слайде (экране) появляются результаты.
Учащимся предлагается выполнить задание с разбором у доски следующего характера: найдите значение выражения
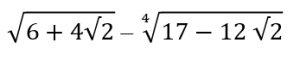
4 Заключительный этап
Организация домашней работы
Дифференцированно. Учащиеся получают задания на карточках (по группам).
Повторить методы (способы) решения иррациональных уравнений.
Группа 1
1) Определите, через какие их данных точек проходит график функции у = :
а) А (27; -3); б) В (-1; 1); в) С (0; 0); г) D (-125; -5).
2) Вычислите:
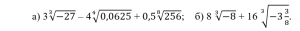
3) Избавьтесь от иррациональности в знаменателе:
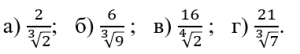
Группа 2
1) Вычислите:
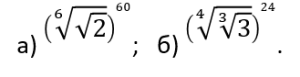
2) Упростите выражение:
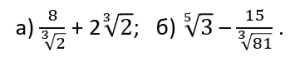
3) Найдите область определения функции:
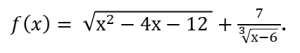
Группа 3
1) Докажите, что значение выражения
![]()
не зависит от значения переменной.
2) Найдите значение выражения

3) Найдите естественную область определения функции
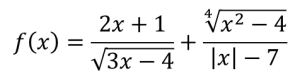
Подведение итогов. Выставление отметок
Учащиеся по очереди вытягивают из корзины листочки с записанными ранее ими задачами (задача может оказаться любого из одноклассников, не обязательно своя), зачитывают и делают отметку о выполнении данной задачи.
Далее комментируются отметки за урок с учётом работы во время урока и результатов теста.
Рефлексия (Слайд 7)
Учащимся предлагается выбрать начатое предложение и продолжить его:
– Сегодня я узнал …
– Сегодня было интересно …
– Было трудно …
– Я выполнял задания …
– Я понял, что …
– Теперь я могу …
– Я почувствовал, что …
– Я научился …
– У меня получилось …
– Я смог …
– Я попробую …
– Меня удивило …
– Урок дал мне для жизни …
– Мне захотелось …



 Предложить публикацию
Предложить публикацию