Моделирование как метод развития навыков решения текстовых задач на I ступени общего среднего образования. Описание опыта педагогической деятельности

Развитие навыков решения текстовых задач – это залог успешного обучения учащихся на ΙΙ и ΙΙΙ ступенях общего среднего образования не только по математике, но и по другим школьным предметам (физике, химии, биологии).

Ольга ФИЛОНЕНКО,
учитель начальных классов
ГУО «Средняя школа № 2 г. Наровли имени И.М.Шаврея»,
Гомельская область

Одной из главных задач, поставленных сегодня перед педагогами, является повышение качества образования. В системе учебных предметов математике как важнейшей составляющей интеллектуального развития школьников принадлежит особая роль. Успешность детей в изучении этого учебного предмета на Ι ступени общего среднего образования во многом зависит от умения решать текстовые задачи, которые способствуют развитию логического мышления и творческих способностей учащихся. Заметила, что первые шаги по формированию этого умения не вызывают у первоклассников особых затруднений. Однако в дальнейшем самостоятельное решение составных задач становится для многих учащихся сложным, а порой и непосильным заданием. Переходя из класса в класс, многие дети начинают испытывать всё большие трудности. Таким ребятам сложно воспринимать и осмысливать условие задачи, определять отношения между известным и искомым, устанавливать необходимую взаимосвязь, ведущую к выбору действия для решения задачи. Между тем развитие навыков решения текстовых задач – это залог успешного обучения учащихся на ΙΙ и ΙΙΙ ступенях общего среднего образования не только по математике, но и по другим школьным предметам (физике, химии, биологии).

Я пришла к выводу, что использование традиционных методов и приемов обучения младших школьников решению текстовых задач не всегда позволяет выйти на желаемый результат. Возникла необходимость в совершенствовании работы над задачей через поиск более эффективных методов. Решение проблемы нашла в применении моделирования – наглядно-практического метода обучения, который в практике школьного обучения получает всё большее признание.

Актуальность выбора темы обусловлена как необходимостью повышения качества математического образования, так и существующими в современной педагогической практике противоречиями. Сегодня практическое применение моделирования в начальной школе носит эпизодический и бессистемный характер и считается многими педагогами малоэффективным. Между тем действующие учебные программы по математике требуют развития у учащихся самостоятельности при решении текстовых задач [2, с. 7]. Каждый выпускник начальной школы должен уметь кратко записывать условие задачи, иллюстрируя ее с помощью рисунка, чертежа или схемы, обосновывать выбор арифметических действий и последовательность их выполнения, проверять правильность решения. Однако на практике этими умениями и навыками владеют далеко не все учащиеся.

Исходя из актуальности темы, мною была определена цель опыта – развитие навыков решения текстовых задач на I ступени общего среднего образования с помощью метода моделирования.

В соответствии с целью были поставлены следующие задачи:

– создать условия для формирования у учащихся навыков построения и чтения простейших моделей текстовых задач через использование математической символики;

– определить эффективность метода моделирования при решении текстовых задач разных видов;

– проанализировать результативность использования моделирования при решении текстовых задач посредством мониторинга результатов контрольных работ.

Решению поставленных задач способствовали следующие методы: теоретический (анализ литературы по теме опыта), практический (составление дидактических заданий по работе с учебными моделями; разработка фрагментов учебных занятий с использованием метода моделирования; создание копилки дидактического материала); исследовательский (анализ контрольных работ).

Описание опыта педагогической деятельности

Математика – это наука, оперирующая абстрактными понятиями. Многие из них трудны для восприятия и понимания учащимися начальных классов.

Широкие возможности для развития навыков решения задач дает моделирование, которое помогает ребенку не только осмыслить, наглядно представить сюжет, но и самому найти рациональный способ решения [2, с. 4]. В основу этого метода положен принцип замещения реальных предметов действиями с уменьшенными образцами: моделями, макетами, муляжами, а также графическими заменителями – рисунками, чертежами (при соблюдении масштаба), схемами (без соблюдения масштаба). В роли моделей в данном случае выступают не конкретные предметы, о которых говорится в задаче, а их заменители (точки, отрезки, палочки, геометрический материал). «Уровень владения моделированием определяет успех решающего задачу», поэтому «обучение моделированию должно занимать главное место в формировании умения решать задачи» [3, с. 26].

Вопросам решения текстовых задач с помощью метода моделирования посвящены работы А.К.Артёмова [1, с. 21], А.А.Столяра [3, с. 76], Л.Ф.Обуховой [8, с. 357], М.А.Бородулько [3, с. 76], Л.П.Стойловой, В.Л.Дрозд [6, с. 77], А.Т.Катасоновой, М.А.Урбан, Е.Н.Трич [9, с. 72–75], С.Е.Царевой [7, с.  220], Г.Л.Муравьёвой и других.  

Идеи этих авторов помогли мне определить этапы работы над текстовой задачей с применением моделирования и позволили выстроить определенную систему в работе. Как правило, при обучении детей решению текстовых задач с помощью метода моделирования сначала провожу подготовительную работу, затем организую непосредственное обучение моделированию текстовых задач и закрепляю умения решать различные виды задачи с помощью моделирования.

В 1-м классе особое внимание уделяю подготовке учащихся к решению задач. Первостепенное значение придаю созданию условий для формирования у первоклассников навыков осознанного чтения: четкого понимания смысла действий «сложение», «вычитание», отношений «больше на…», «меньше на…», разностного сравнения; отработке умений анализировать, сравнивать, классифицировать, обобщать, делать соответствующие выводы, пользуясь при этом предметной наглядностью и графическими моделями.

Во 2-м классе осуществляю формирование у детей обобщенных умений решать простые и составные задачи на сложение и вычитание, а также знакомлю с задачами, в которых раскрывается конкретный смысл умножения и деления.

В 3–4-м классах формирую общеучебные умения решать задачи на увеличение и уменьшение числа в несколько раз («больше в…», «меньше в…») и кратного сравнения; решать и составлять обратные задачи на умножение и деление, знакомлю с задачами на движение.

Чтобы научить детей решать различные виды задач, сначала организую работу, направленную на формирование необходимых обобщенных умений: внимательно читать текст задачи; выделять условие и требование задачи (что известно и что нужно найти); устанавливать взаимосвязь между известными и неизвестными величинами; составлять план по выбору необходимых действий для поиска ответа на вопрос задачи; определять способы проверки решения.

Для лучшего усвоения алгоритма решения задачи предлагаю учащимся пользоваться индивидуальной памяткой «Советы мудрой тётушки Совы» (Приложение 1).

Благодаря такому подходу при решении арифметических задач на уроках математики младшие школьники осваивают четыре основных вида моделей: предметные, вербальные, схематические, математические.

Предметные модели помогают представить сюжет и отображают количество предметов и отношения между ними.

Например, для решения задачи (1-й класс) «У Дианы было 3 яблока, а у Пети на 4 яблока больше. Сколько яблок у Пети?» [6, с. 64] использую такую модель:

Далее для решения этой же задачи применяю один из видов вербальных моделей, когда текст задачи в первичном, не обработанном виде, трансформируется в краткую запись сюжета и краткую запись условия задачи в виде таблицы – более абстрактной модели. Например:

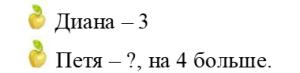
Для решения задачи (2-й класс) «В одном пенале 2 ручки. Сколько ручек в 3 таких пеналах?» применяю следующую таблицу-модель:

Использование схематических моделей позволяет мне помочь учащимся лучше представить и осмыслить условие, где конкретные предметы представлены условными обозначениями: отрезками и геометрическим материалом. Примером решения вышеуказанной задачи с яблоками могут служить следующие модели:

– схематическая иллюстрация:

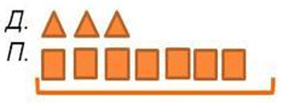
– схематические чертежи

Математические модели применяю при решении равенства или выражения, которые в цифровой форме показывают отношения между данными и искомым, буквенные выражения и уравнения [8, с.  288].

Например,

При анализе задачи предлагаю детям сразу несколько моделей. Каждый учащийся самостоятельно определяет, какая модель ему более доступна и понятна для осмысления.

Чтобы решить любую задачу, развиваю у детей умение переходить от текста задачи (словесной модели) к представлению ситуации (мысленной модели), а от неё – к записи решения с помощью математических символов (знаково-символической модели). Чтобы работа с моделями дала желаемый результат, применяю их последовательно и систематически.

Начиная обучение решению простых задач с использованием моделей в первом классе, обязательно учитываю возрастные особенности младших школьников, у которых наглядно-действенное, наглядно-образное и словесно-логическое мышление формируются последовательно, дополняя их интеллектуальные возможности.

Методику обучения младших школьников моделированию текстовых задач реализую поэтапно. Сначала провожу подготовительную работу к моделированию текстовых задач через:

а) развитие графических навыков (отработку умений пользоваться линейкой и карандашом, чертить отрезки, прямые, ставить заданные точки);

б) развитие зрительного восприятия (совершенствование умения определять длину отрезков и сравнивать их на глаз);

в) развитие мышления, т.к. для самостоятельного выполнения даже самого элементарного задания необходимо осмысление (Приложение 2).

Далее, апеллируя к трём видам мышления, действую по принципу: от простого к сложному, от абстрактного к конкретному, от предметного моделирования к схематическому.

Представлю систему своей работы на каждом этапе [7, с. 7] на конкретных примерах.

1-й этап – работа с «подвижной» схемой, основанной на наглядно-действенном мышлении. На данном этапе в качестве средств моделирования использую счётный геометрический материал, который учащиеся могут свободно перемещать руками на парте (это могут быть любые предметы, заменяющие реальные объекты: пуговицы, счётные палочки или счётный материал в виде геометрических фигур, фишки и т.п.). Сначала предлагаю детям выполнить практическую работу по выбору действий при решении задач, а затем прошу учащихся сделать обоснованный вывод (Приложение 3).

Такой подход, как показала моя практика, приводит к тому, что в дальнейшем ребята учатся управлять своими действиями самостоятельно, осуществляя не случайные, а целенаправленные поиски способа решения задачи. Манипуляции предметами становятся своего рода основой для понимания математики.

2-й этап – работа со схематической иллюстрацией, основанной на наглядно-образном мышлении. Если дети хорошо освоили приём решения задач с помощью манипулирования предметами, то теперь они могут это представить в уме. Используя листы бумаги, учу школьников решать задачи с помощью схематических иллюстраций. При построении предлагаю использовать как геометрические фигуры, так и штрихи-палочки (с ними работать удобнее). Ребята представляют действие в виде стрелки или перечёркивания, что помогает им лучше запомнить образ того действия, которое нужно выполнить (Приложение 4).

3-й этап – работа со схематическим чертежом, начинаю ее после ознакомления с понятием «отрезок». К схематическому моделированию перехожу в том случае, если учащиеся овладели мысленной манипуляцией предметами и научились выбирать нужный знак действия для решения задачи. Для этого, используя доску и листы в крупную клеточку или листы с пунктирной основой, учу ребят строить схематические чертежи, «схемы», без соблюдения масштаба. При этом обращаю внимание детей на то, что количество изображаемых отрезков обязательно должно соответствовать численности множеств, описанных в задаче. С увеличением числовых данных работа по обучению моделированию основывается на вычерчивании схематических чертежей, которые условно передают численность представленных в задаче множеств (Приложение 5).

Далее учу детей выстраивать схематические модели с использованием необходимых символов и знаков: ^, –, ∆. Знакомлю с понятиями «целое», «часть» и «количество частей», показываю, как пользоваться формулами-подсказками, «Волшебным треугольником» для построения и нахождения правильного способа решения различных видов задач (Приложения 6, 7).

Чтобы решать задачи самостоятельно, ученик должен освоить разные виды моделей, научиться выбирать ту модель, которая будет соответствовать предложенной задаче, при необходимости переходить от одной модели к другой. Сделать процесс последовательным и эффективным мне помогают следующие группы заданий:

1. Задания на соотнесение моделей, предполагающие сравнение ребенком текста задачи, рисунка, схемы и числового выражения и пояснения им соответствия моделей друг другу. Для это могу спросить у детей, подходит ли рисунок к задаче, подходит ли краткая запись к рисунку, подходит схема к рисунку, верно ли составлено числовое выражение к задаче и т.п. (Приложение 8).

2. Задания на выбор модели. Они предполагают, что ребёнок из нескольких вариантов предложенных моделей одного вида должен выбрать ту, которая подходит к условию данной задачи. Чтобы выполнять такие задания, ученики должны уметь соотносить одну модель с другой. Для этого прошу их выполнить следующие виды работ: выбрать схему, которая соответствует иллюстрации или условию задачи; выбрать ту задачу, которая соответствует схеме или выражению и т. п. (Приложение 9).

3. Задания на изменение модели. Под ними следует понимать внесение в предложенную модель определённых изменений так, чтобы она стала соответствовать другим требованиям или другой предложенной модели. Для выполнения такого рода заданий предлагаю детям дополнить модель недостающими данными, удалить из модели лишние данные, исправить схему так, чтобы она соответствовала условию и т.п. (Приложение 10).

4. Задания на построение модели направлены на формирование у ребёнка умения самостоятельно выстраивать модель определённого вида, которая будет подходить к определенной задаче. Использую следующие виды таких заданий: составить схему к рисунку или, наоборот, сделать рисунок к данной схеме; придумать задачу по рисунку или сделать рисунок к краткой записи; составить задачу по данной схеме; составить пример к рисунку; придумать задачу, которая будет решаться с помощью следующего действия: «18-10=?»; составить схему к выражению или выражение по схеме и др. (Приложение 11).

Заметила, что освоение метода моделирования при решении простых задач снимает необходимость готовить учащихся к решению составных задач как к чему-то новому. Они без особых затруднений переносят свои умения на решение составных задач различных видов. Далее схематические чертежи использую для моделирования задач на движение двух тел, где расстояние и время отображаются в виде отрезков, а скорость и направление движения – в виде стрелки (вектора).

Результативность и эффективность опыта

Обобщая полученные результаты, могу говорить о том, что моделирование является наиболее эффективном методом для развития навыков решения текстовых задач по математике. Оно позволяет прочно усвоить, углубить и закрепить предметные знания, развить необходимые умения и навыки учащихся, является одним из способов формирования познавательной активности школьников, влияет на развитие их интеллектуальных способностей.

Работая над опытом, я заметила, что процесс моделирования повышает активность учащихся на уроке, содействует развитию логического и абстрактного мышления, способствует прочному усвоению общего приёма работы над задачей. Кроме того, моделирование учит детей «строить» задачи, помогает аргументировано излагать свои мысли, работать самостоятельно. Введение в образовательный процесс моделей и моделирования существенно меняет отношение учащихся к учебному предмету, делает учебную деятельность более осмысленной и продуктивной.

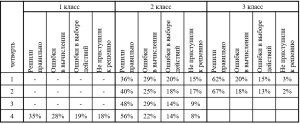
Эффективность опыта очевидна. Она подтверждается ростом количества учащихся, умеющих самостоятельно решить текстовую задачу без ошибок в выборе действия и вычислениях, положительной динамикой качества знаний учащихся по математике (Приложение 12). Это, в свою очередь, отражается и на результатах внеклассной деятельности по предмету. В течение трех лет мои учащиеся являются активными участниками интеллектуальной игры-конкурса «Кенгуру». В 2022/2023 учебном году стали дипломантами районного этапа детского конкурса интеллектуалов «ДетКИ» (диплом ΙΙ степени). Активно участвуют в школьных олимпиадах, викторинах и математических рингах.

Деятельность по развитию навыков решения задач с помощью моделирования одобрена коллегами-учителями. Данный опыт был представлен на заседаниях школьного и районного методических объединений, заслушивался на педагогическом совете. Считаю выбранное направление работы перспективным и планирую продолжить его. Хотела бы рекомендовать опыт работы для использования своим коллегам – учителям начальных классов и учителям математики.

Приложение 1

Советы мудрой тётушки Совы. Памятка для учащихся

1. Внимательно прочитай задачу. Уясни, что тебе известно и что нужно найти

2. Сделай чертёж, иллюстрацию или краткую запись к задаче. Обозначь все известные (данные) и неизвестные (искомые) величины

3. Составь план решения. Подумай, каким действием нужно решать. Что и в какой последовательности нужно находить. Объясни почему.

4. Запиши решение, найди ответ

5. Проверь решение и полученный ответ

Приложение 2

Подготовительные упражнения на развитие графических навыков

1. Определи на глаз, какой отрезок самый длинный, к какой самый короткий. Проверь себя с помощью нити или полоски бумаги.

2. Нарисуй на листе бумаги точку. Проведи через нее две прямые линии;

3. Нарисуй на листе бумаги две точки. Согни лист этой бумаги так, чтобы точки находились на линии сгиба;

4. Нарисуй на листе бумаги две полоски: красную длиной 4 см и шириной 1 см, и синюю длиной 6 см и шириной 2 см.;

5. Нарисуй три треугольника и два квадрата. Объедини их к замкнутой кривой линией;

6. Начерти на листе бумаги отрезок. Поставь: точку В ближе к середине отрезка; точку С ближе к началу отрезка; точку А ближе к концу отрезка;

7. Начерти на листе бумаги отрезок длиной 8 см, раздели его на 2 равные части.

Приложение 3

1-й этап. Работа с «подвижной схемой» для выбора действия (фрагмент урока)

Росло 3 красных тюльпана и 2 жёлтых. Сколько тюльпанов было всего? [10, с. 31]

После чтения задачи и её анализа на наборном полотне демонстрирую, а затем прошу ребят сделать то же самое у себя за партами.

Учитель. Положите перед собой столько треугольников, сколько росло красных тюльпанов. Рядом положите столько квадратов, сколько росло жёлтых тюльпанов. Как узнать, сколько всего росло тюльпанов? (Ответ учащихся. Множество предметов нужно объединить).

Учитель. Действительно, нужно объединить два множества предметов. Давайте сделаем это (учитель на доске, дети на парте придвигают группы фигур).

Учитель. Какой вывод мы можем сделать? (Ответы учащихся).

Учитель (подводя итог сказанного детьми). Мы придвинули фигуры, а это означает, что выполнили сложение, которое обозначается знаком «+». Две части объединили в одно целое, т.е. к трём придвинули (прибавили) два. Давайте запишем решение в виде числового выражения (Дети делают запись 3 + 2 = 5 в тетради, учитель или ученик записывает решение на доске) и сформулируем ответ.

Параллельно из предложенных мною глаголов «положили», «отдала», «взяли», «приплыло» «отрезали», «прилетело» дети выбирают те, которые соответствуют данному практическому действию и смыслу – «стало больше». Таким образом, дети решают задачи на нахождение суммы.

Аналогичным способом анализируются задачи на нахождение разности: удалили подмножество из данного множества, забрали часть от целого. Задача решается вычитанием, которое записывается с помощью знака «–».

Приложение 4

2-й этап. Работа со схематической иллюстрацией. Задачи на нахождение разности

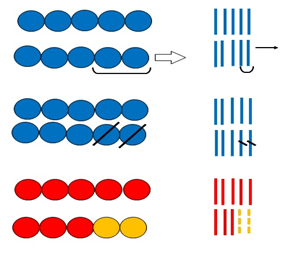
На тарелке лежало 7 яблок. Взяли 2 яблока. Сколько яблок осталось на тарелке? (Нарисуй столько палочек, сколько яблок лежало на тарелке. Сколько яблок взяли? Покажи на схеме, что 2 яблока взяли. Как это можно сделать? Можно зачеркнуть 2 палочки, а можно показать стрелочкой, что их взяли).

Задачи на нахождение суммы

На тарелке лежало 5 груш. К ним положили ещё 2 яблока. Сколько фруктов стало на тарелке?

Аналогично иллюстрируются и разбираются задачи на увеличение (уменьшение) числа на несколько единиц.

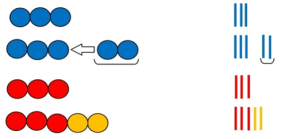
У Кати 3 карандаша, а у Лены на 2 карандаша больше. Сколько карандашей у Лены?

У Кати 5 карандашей, а у Лены на 2 карандаша меньше. Сколько карандашей у Лены?

Приложение 5

3-й этап. Работа со схематическим чертежом (фрагмент урока)

У Кати было 3 матрёшки. А у Даши на 2 матрёшки больше. Сколько матрёшек было у Даши? [6 с. 134 №1].  

Учитель. Сколько матрёшек было у Кати?

Учащиеся. У Кати было 3 матрёшки.

Учитель. Нарисуй столько отрезков, сколько матрёшек было у Кати.

Учитель. Сколько матрёшек было у Даши?

Учащиеся. У Даши было на 2 матрёшки больше.

Учитель. Что это значит?

Учащиеся. У Даши было столько же, как и у Кати, да ещё 2.

Учитель. Покажи это на чертеже. (Под первым чертежом дети рисуют 3 отрезка и ещё 2). Каким действием будет решаться эта задача?

Учащиеся. Сложением.

Приложение 6

Задача на нахождение неизвестного уменьшаемого (фрагмент урока)

Когда кот съел 6 рыбок из тарелки, там осталось ещё 2 рыбки. Сколько рыбок было в тарелке сначала?

Обычно слова «осталось», «съел», «утащил» ассоциируются у детей с уменьшением, и подталкивают детей к выбору ошибочного действия при решении. Построение схемы исключает такую ошибку.

Применяю приём «порционного» чтения.

Учитель. Прочитаем задачу. О чём говорится в задаче? Что вы представили?

Учащиеся. О рыбках, которые были в тарелке. Их оттуда брал кот.

Учитель. Все рыбки утащил кот?

Учащиеся. Нет, там ещё остались рыбки.

Учитель. Что означает число 6? 2?

Учащиеся. 6 – это столько рыбок съел кот, 2 – столько рыбок осталось.

Учитель. Что надо узнать в задаче? Какое здесь требование?

Учащиеся. Надо узнать, сколько рыбок было в тарелке сначала.

Учитель. Изобразим эту ситуацию на схеме? Сколько у нас тарелок описано в задаче?

Учащиеся. Одна, так как кот брал рыбок из одной тарелки.

Учащиеся. Чертим отрезок – это тарелка с рыбками. 6 рыбок забрали. Показываем эту часть, делаем штришки-зарубочки, показываем, что это рыбки, которые забрали.

Остальная часть – это рыбки, которые остались в тарелке, их 2.

Надо найти, сколько рыбок было в тарелке сначала. Ставим вопрос ?

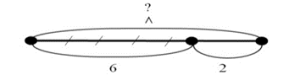
Учитель. Чем являются числа 6 и 2 на отрезке?

Учащиеся. Это части, которые составляют целое. (Обозначают значками ? и ^)

Учитель. Как же найти целое?

Учащиеся. Чтобы найти целое, надо части сложить.

Учитель. Запишите математическое выражение.

Учащиеся. 6 + 2 = 8 (р.) или 2 + 6 = 8 (р.).

Учитель. Какой был вопрос в задаче? Как вы ответите на поставленный вопрос?

Приложение 7

Моделирование   простых текстовые задачи на сложение и вычитание

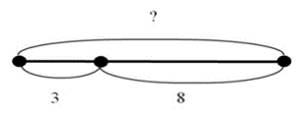
1. Лена съела 3 конфеты, а Дима – 8. Сколько конфет съели дети? Нахождение суммы: 3 + 8 = 11 (конфет)
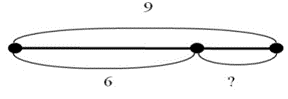
2. В вазе 9 цветов. Из них 6 тюльпанов, остальные нарциссы. Сколько нарциссов в вазе? Слагаемого: 9 – 6 = 3 (нарцисса)
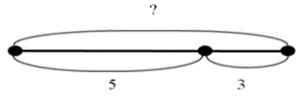
3. Шмель пролетел 5 метров от клумбы. Ему осталось ещё 3 м до следующей клумбы. Сколько метров составил весь путь шмеля? Уменьшаемого: 5 + 3 = 8 (м)
4. На ветке сидело 12 птиц. Когда несколько птиц улетело, их осталось 4. Сколько птиц улетело? Вычитаемого: 12 – 4 = 8 (птиц)
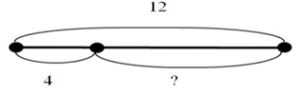5. На пляже загорало 14 ребят. 11 ушли купаться. Сколько ребят осталось загорать? Остатка: 14 – 11 = 3 (ребят)

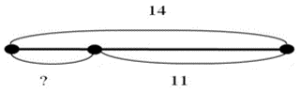Простые задачи на увеличение/уменьшение числа на несколько единиц

1. В корзинке 3 яблока, а на ветке на 5 яблок больше. Сколько яблок на ветке?
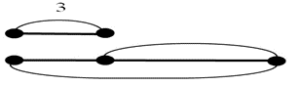2. В пенале 7 фломастеров, на столе – на 4 меньше. Сколько фломастеров на столе?

Простые задачи на разностное сравнение

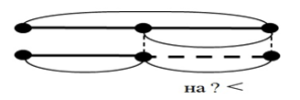
1. Тане 9 лет, а Мише 4 года. На сколько Таня старше Миши?
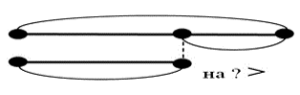2. В одной раскраске 16 картинок, а в другой – 8. На сколько картинок во второй раскраске меньше, чем в первой?

Приложение 8

1. Задания на соотнесение нескольких моделей к одной задаче

Цель этих заданий – научить ребёнка сравнивать между собой предложенные модели и устанавливать их соответствие или несоответствие, т. е ученик должен уметь объяснить, почему схема «подходит» или «не подходит» к равенству и рисунку.

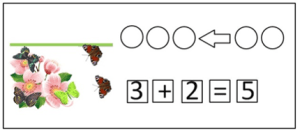
Можно предложить следующие задания:

– Подходит ли к задаче рисунок? (Сравнение вербальной и предметной моделей).

– Подходит ли схема к рисунку? (Соотнесение предметной и схематической моделей).

– Правильно ли составлено числовое выражение к рисунку? Почему? (Соотнесение предметной и математической модели).

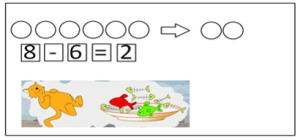
Приложение 9

2. Задания на выбор необходимой модели

Чтобы выполнять данный вид заданий, учащиеся должны уметь определять соответствие одной модели другой.

– Выбери схему, которая соответствует условию задачи (сюжетной иллюстрации, числовому выражению);

– Выбери из предложенных иллюстраций ту, которая соответствует схеме (тексту, или числовому выражению);

– Выбрать из нескольких условий то, которое соответствует схеме (сюжетному рисунку или числовому выражению).

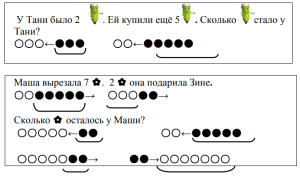
Приложение 10

3. Задания на изменение модели

При выполнении заданий этого вида ученикам нужно внести изменения в данную модель так, чтобы она стала соответствовать другим требованиям или другой предложенной модели.

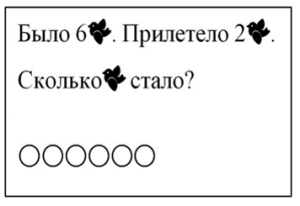
Это, по сути, задания трёх видов:

1) Задания на дополнение модели недостающими элементами

– Измени схему так, чтобы она соответствовала тексту задачи (сюжетной иллюстрации или числовому равенству).

– Измени условие задачи так, чтобы оно соответствовало сюжетной иллюстрации или числовому равенству, выражению.

2) Задания на удаление из текста задачи лишних данных  (на изменение вербальной модели). После решения задачи учащиеся изменяют текст задачи в соответствии с математической моделью так, чтобы не было лишних данных.

3) Задания на исправление моделей (замену одних элементов другими).

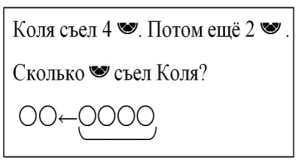
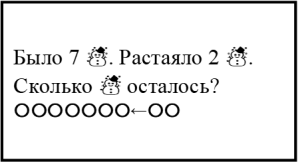
– Исправьте предложенную схему так, чтобы она соответствовала тексту задачи (вербальной модели).

Приложение 11

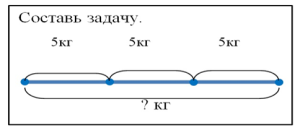
4. Задания на построение модели

 Эти задания направлены на формирование у ребёнка умения самостоятельно выстраивать модель определённого вида, которая будет подходить к этой задаче.

– Составь схему, соответствующую рисунку, тексту или числовому выражению.

– Составь задачу по схеме, рисунку или числовому выражению.

– Сделайте рисунок к тексту задачи.

– Составьте пример к рисунку, тексту или схеме.

Приложение 12

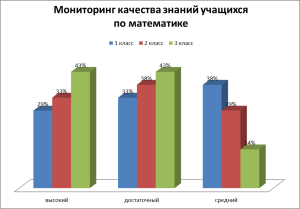
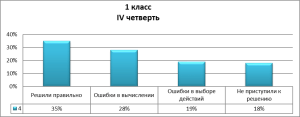
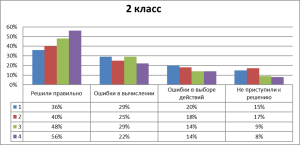
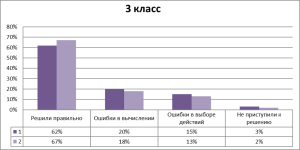
Результативность контрольных работ

Список использованных источников

1 Артёмов, А.К. Формирование обобщённых умений решать задачи / А.К.Артёмов / Начальная школа, – 1992. – № 2. – с. 21.
2 Бородулько, М.А. Обучение решению задач и моделирование/М.А.Бородулько, Л.П. Стойлова. – Начальная школа. – 1996. – № 8.
3 Дрозд, В.Л. Практикум по методике начального обучения математике: Для пед. ин-тов по спец. 2121 «Педагогика и методика нач. обучения / В.Л.Дрозд [и др.]. – Минск : Высшая школа. – 1984. – 97 с.]
4 Левенберг, Л.Ш. Рисунки, схемы и чертежи в начальном курсе математики / Л.Ш.Левенберг. – М., 1978. – 27 с.
5 Морозов, К.Е. Математическое моделирование в научном познании / К.Е.Морозов. – М. : Мысль. – 1969. – c. 7
6 Нефедова, Е.А. 2000 задач и примеров по математике / Е.А.Нефедова, О.В.Узорова. – М. : Просвещение. – 1992.
7 Николаева, В.В. 1300 задач и примеров по математике для начальных классов. / Авт. –сост. В.В.Николаева, Т.М.Чеботаревская. – Минск : Юнипресс. – 2005. 
8 Обухова, Л.Ф. Детская психология: теория, факты, проблемы / Л.Ф.Обухова. – М. : Тривола, 1995. – 357 с.
9 Салмина, Н.Г. Знак и символ в обучении / Н.Г.Салмина. – М. : МГУ,1988. – 288 с.
10 Чеботаревская, Т.М. Математика: учебник для 1 класса общеобразовательных учреждений с русским языком обучения. В 2 ч. Ч. 1 / Т.М.Чеботаревская. – Минск : Народная асвета, 2012. –56 с.
11 Чеботаревская, Т.М. Математика: учебник для 2 класса общеобразовательных учреждений с русским языком обучения. В 2 ч. Ч. 2 / Т.М.Чеботаревская. – Минск : Народная асвета, 2012. –31 с.

Поделиться ссылкой: