Выкарыстаныя тэхналогіі: праблемнае навучанне, крытычнае мысленне, камунікатыўныя зносіны. Формы арганізацыі вучэбнай дзейнасці: франтальная, групавая, індывідуальная.
 Рамуальда МАХНАЧ,
Рамуальда МАХНАЧ,
настаўнік матэматыкі
ДУА “Трабская сярэдняя школа”
Іўеўскага раёна,
Гродзенская вобласць
Тып урока: урок першапачатковага фарміравання ўменняў і навыкаў.
Метады: часткова-пошукавы.
Выкарыстаныя тэхналогіі: праблемнае навучанне, крытычнае мысленне, камунікатыўныя зносіны.
Формы арганізацыі вучэбнай дзейнасці: франтальная, групавая, індывідуальная.
Абсталяванне:
– Алгебра: вучэбны дапаможнік для 10 класа ўстаноў агульнай сярэдняй адукацыі з беларускай мовай навучання / І.Г.Арэф’ева, В.М.Пірутка. – Мінск: Народная асвета, 2019;
– праграма “GeoGebra” (https://www.geogebra.org/graphing, або можна спампаваць версію на рускай мове http://www.anyaplanet.net/learning/GeoGebra.html);
– транспарант “Графікі і ўласцівасці трыганаметрычных функцый” (можна спампаваць тут: https://drive.google.com/file/d/1KZ2DhnVd5ZDs1fR01C5utr2cPb6lnalg/view?usp=sharing);
– прэзентацыя “Функцыя у = sin x. Уласцівасці і графікі”
(https://docs.google.com/presentation/d/1qcvAdT6fywdhlFrgvgxCm5_CddXjFpwMbvA267HPk0A/edit#slide=id.p1);
– інтэрактыўная дошка;
– камп’ютары;
– табліца “Трыганаметрычны круг”;
– раздатачны матэрыял.
Мэта ўрока:
– знаёмства вучняў з уласцівасцямі функцыі у = sin x, навык пабудавання і чытання графіка функцыі у = sin x;
– фарміраванне ў вучняў практычных навыкаў па аналізе і апрацоўцы інфармацыі пры вывучэнні тэмы “Функцыя y=sinx. Уласцівасці і графік”.
Задачы ўрока:
навучальная:
– фарміраваць уменне пабудовы графіка функцыі у = sin x, навыкі чытання графікаў, вызначэнне ўласцівасцей функцыі;
развіваючыя:
– спрыяць развіццю ўвагі, лагічнага мыслення, матэматычнай мовы, умення аналізаваць, абагульняць і прымяняць веды ў нестандартных сітуацыях;
выхаваўчыя:
– актывізаваць цікавасць да атрымання новых ведаў,
– выхоўваць графічную культуру, фарміраваць дакладнасць і акуратнасць пры выкананні чарцяжоў;
– выхоўваць культуру калектыўных зносін, здольнасці адстойваць сваё меркаванне, слухаць аднакласнікаў, прызнаваць свае памылкі.
Ход урока
І Арганізацыйна-матывацыйны этап
Настаўнік: У старажытнагрэчаскага вучонага Фалеса спыталі:
– Што большае за ўсё на свеце?
– Прастора.
– Што хутчэй за ўсё?
– Розум.
– Што мудрэй за ўсё?
– Час.
– Што прыемней за ўсё?
– Дасягнуць жаданага.
Я вітаю вас на ўроку алгебры. Жадаю вам у прасторы гэтага кабінета за абмежаваны час нашага ўрока з дапамогай вашага розуму дасягнуць жаданага. Гэта значыць вырашыць усе задачы, якія сёння будуць стаяць перад намі.
Тэма нашага ўрока, як вы напэўна ўжо заўважылі “Функцыя у = sinx. Уласцівасці і графік”. І зараз давайце разам сфармулюем задачы, якія мы паставім перад сабой і пастараемся дасягнуць іх на сённяшнім уроку. Калі ласка. (Настаўнік выслухоўвае і карэкціруе прапановы вучняў).
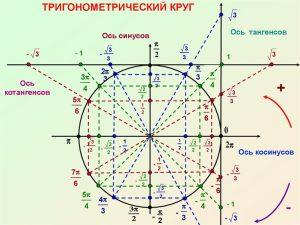
Настаўнік: Вядомы савецкі фізіёлаг Іван Пятровіч Паўлаў гаварыў: “Вывучайце азы навукі. Перш чым узысці на яе вяршыні, ніколі не бярыся за наступнае, не засвоіўшы папярэдняе”, – а таму пачнём урок з паўтарэння. Адзінкавая трыганаметрычная акружнасць, трыганаметрычны круг нам добра знаёмыя. Адкажыце калі ласка на наступныя пытанні (вучні працуюць па табліцы “Трыганаметрычны круг):
– Чаму дадзеная акружнасць называецца адзінкавай?
– На якой каардынатнай восі паказаны значэнні сінуса адвольнага вугла?
– Якія значэнні можа прымаць сінус адвольнага вугла?
– У якіх каардынатных чвэрцях сінус прымае дадатныя значэнні? Адмоўныя?
– Сінус якіх вуглоў роўны нулю?
– Сінус якіх вуглоў можна вызначыць дакладна па трыганаметрычнай акружнасці?
– Дайце азначэнне функцыі.
– Якія ўласцівасці адвольнай функцыі мы вызначаем пры яе даследаванні? (Абсяг вызначэння, мноства значэнняў, нулі функцыі, прамежкі знакапастаянства, манатоннасць функцыі, найбольшае і найменшае значэнні функцыі, цотнасць).
Запішыце ў сшытках у пранумараваны слупок гэтыя ўласцівасці. Апошняй у слупку напішыце літару Т. (Адзін вучань робіць запіс на дошцы, астатнія ў сшытках)
ІІ Аперацыйна-пазнавальны этап
Вывучэнне новага матэрыялу
Пераходзячы да наступнага этапа ўрока, я хачу працытаваць вядомага французскага матэматыка Рэнэ Дэкарта, які сцвярджаў: “Для таго каб удасканальваць розум, патрэбна больш разважаць, чым завучваць”.
Завучаны матэрыял мы паўтарылі, а зараз будзем разважаць. Увага на інтэрактыўную дошку. Разгледзім пабудаванне графіка функцыі y = sinx з прымяненнем трыганаметрычнага круга. Па графіку апішам усе ўласцівасці функцыі. (Адзін вучань робіць запіс на дошцы, астатнія – у сшыткі ў падрыхтаваныя шаблоны)
Засваенне новых тэрмінаў: графік функцыі – сінусоіда, новая ўласцівасць функцый – перыядычнасць.
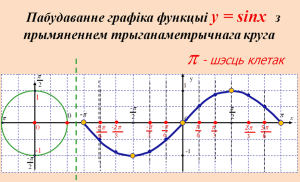
Яшчэ раз паўторым і замацуем.
А цяпер разгледзім пабудаванне графікаў шляхам пераўтварэння. Звярніце ўвагу, якія ўласцівасці функцыі змяняюцца пры гэтым.
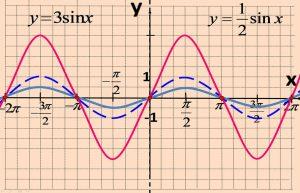
Практычнае прымяненне
Настаўнік:
І хваляю лінія гэта качаецца,
І сінусам графік яе называецца,
Праз пэўны перыяд яна паўтараецца,
І тройчы нулю ў перыяд раўняецца.
Яна паўперыяда ўверх падымаецца,
Трапляе ў адзінку і ўніз апускаецца.
Ля восі абсцыс хваляй так і ўздымаецца
У сістэме, якую стварыў нам Дэкарт.
Дарэчы, сучасны выгляд трыганаметрыі надаў найбуйнейшы матэматык васямнаццатага стагоддзя Л.Эйлер. Ён увёў вядомыя азначэнні трыганаметрычных функцый, стаў разглядаць функцыі адвольнага вугла, атрымаў формулы прывядзення. Пачынаючы з XVII ст., трыганаметрычныя функцыі пачалі ўжываць для рашэння ўраўненняў, задач механікі, оптыкі, электрычнасці, радыётэхнікі, для апісання вагальных працэсаў, распаўсюджвання хваль, руху розных механізмаў, для вывучэння пераменнага электрычнага току і г. д. Таму трыганаметрычныя функцыі ўсебакова і глыбока даследаваліся і набылі важнае значэнне для ўсёй матэматыкі.
Фізкультхвілінка
Давайце крышку адпачнём і зробім гімнастыку для вачэй па трэнажоры.
Настаўнік: Прыменім набытыя тэарэтычныя веды на практыцы і выканаем заданні з падручніка.
Заданні № 1.154, 1.155, 1.156 (вусна),
Заданні № 1.157, 1.159, 1.168 (з тлумачэннем на дошцы)
Настаўнік: Старажытная мудрасць вучыць нас: “Скажы мне, і я забуду, Пакажы мне, і я запомню, Зацікаў мяне, і я навучуся”. Лічу, што яна вельмі пасуе да наступнага этапу нашага ўрока – пабудаванні і даследаванні графікаў функцыі у = sinx у праграме “GeoGebra”. Сядаем за камп’ютары. Увага! Камп’ютар – электронная апаратура, а таму памятаем аб правілах бяспекі падчас работы. Ведайце, што ваша жыццё – самае галоўнае. Беражыце яго.
Фізкультхвілінка
(Уключаецца трэк з гукамі прыроды)
Настаўнік: Самая вялікая нагрузка падчас працы за камп’ютарам прыпадае на зрок і на мозг чалавека. А таму давайце крыху расслабімся і дадзім ім невялічкі адпачынак. Адхіліцеся да спінкі крэсла, закрыйце вочы і ўявіце сабе, што вы ў цудоўным месцы на беразе Клявы, лета, свеціць сонейка. Усміхніцеся яму і падстаўце твар пад яго ласкавыя промні. Вы адпачываеце.
Настаўнік: Яшчэ раз паўторым і назавём усе ўласцівасці функцыі у = sinx: абсяг вызначэння, мноства значэнняў, нулі функцыі, прамежкі знакапастаянства, манатоннасць функцыі, найбольшае і найменшае значэнні функцыі, цотнасць, перыядычнасць.
(Інтэрактыўны транспарант “Графікі і ўласцівасці трыганаметрычных функцый”)
Настаўнік: А цяпер я папрашу вас, абапіраючыся на тэарэтычны і практычны матэрыял, атрыманы падчас урока, праявіць сваю назіральнасць, кемлівасць, творчае мысленне. У мяне ў руках кубік. На кожным баку кубіка напісана адно з заданняў, якое вам трэба выканаць:
1. Апішы гэта … (Апішы форму, памер або іншыя характарыстыкі).
2. Параўнай гэта … (Што падобнае вывучалі?)
3. Праасацыіруй гэта … (Што гэта нагадвае?)
4. Прааналізуй гэта … (Як зроблена? З чаго складаецца?)
5. Прымяні гэта … (Як гэта прымяняецца?)
6. Прывядзіце «за» і «супраць» (Падтрымайце або аспрэчце гэта.)
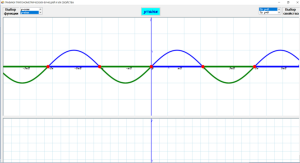
Методыка “Кубік”. Я кідаю кубік над кожным сталом, і такім чынам вызначаецца, у якім ракурсе ваша пара будзе раскрываць паняцце, якое прадстаўлена вашай увазе на слайдзе (сінусоіда). (Вучні характарызуюць сінусоіду)
Пярвічны кантроль
Настаўнік: Старажытнагрэчаскі паэт Нівей сцвярджаў, што матэматыку нельга вывучаць, назіраючы, як гэта робіць сусед. А таму зараз кожны самастойна выканае практычнае заданне на пярвічны кантроль засваення новага матэрыялу. Калі ласка, можаце звяртацца да тэарэтычнага курса, а таксама карыстацца формуламі на дошцы.
Вучні выконваюць заданні з падручніка № 1.158 б) г), № 1.175 з дапаўненнем (пабудаванне графіка і наступнае даследаванне дадзенай функцыі) і ажыццяўляюць самакантроль (звяраюць з эталонам). Выяўляюць памылкі ў выкананні задання, аналізуюць прычыны дапушчаных памылак і магчымыя шляхі іх ліквідацыі.
ІІІ Выніковая рэфлексія
– Што мы рабілі ўдала?
– Што выклікала ў вас цяжкасць?
– Чаму гэта здарылася?
– Над чым, на ваш погляд, варта папрацаваць дома?
IV Дамашняе заданне
Яшчэ раз прачытайце тэарэтычны матэрыял, толькі ўжо па падручніку – § 5, п. 1. Завучыце ўсе асноўныя тэрміны, азначэнні і паняцці.
Выканайце заданне:
1-я група – № 1.207, 1.208, 1.215;
2-я група – № 1.215, 1.220 (па выніках пярвічнага кантролю) .
V Падвядзенне вынікаў урока



 Предложить публикацию
Предложить публикацию