Алла МЕНЬКО,
учитель математики
ГУО «Гимназия № 1 г.Новогрудка»,
Гродненская область
Тема «Сравнение обыкновенных дробей»
Класс: 5
Тип урока: изучение нового материала.
Цели:
Образовательная: сформировать у учащихся умение сравнивать обыкновенные дроби; рассмотреть правила сравнения обыкновенных дробей.
Развивающая: формирование приёмов анализа и синтеза, сравнения, сопоставления, обобщения; развитие математической речи при обосновании каждого шага алгоритма;
Воспитательные: воспитывать настойчивость в овладении правил сравнения дробей; отрабатывать чёткость и последовательность в обосновании действий сравнения дробей.
Ожидаемые результаты
Предполагается, что к окончанию урока учащиеся смогут применять правила сравнения обыкновенных дробей, обосновывать решение задач на сравнение обыкновенных дробей.
Методы: индуктивно-эвристический (по характеру познавательной деятельности), анализ, синтез, сравнение, сопоставление.
Оборудование: листы с заданиями, листы оценивания знаний, презентация, интерактивная доска, учебник «Математика 5 класс».
Формируемые компетенций:
1 Принятие и понимание учебной задачи.
2 Умение строить речевое высказывание в устной и письменной речи.
3 Умение осуществлять анализ с выделением существенных и несущественных признаков и синтез как составление целого из частей.
Ход урока
I Организационно-мотивационный этап.
Проверка готовности к уроку, настрой детей на позитивную работу.
Добрый день, ребята! Сегодня у нас необычный урок. Мы с вами продолжим путешествие по увлекательной стране под названием «Математика». Я очень надеюсь, что вместе с вами мы сможем сделать новые открытия и закрепить изученное. Но в этом путешествии мне будет нужна ваша помощь.
Ну-ка, проверь дружок,
Ты готов начать урок?
Всё ль на месте,
Всё ль в порядке,
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Каждый хочет получать
Только 10 лишь опять.
Ребята, сегодня на уроке мы продолжим изучать обыкновенные дроби, а для этого отправимся в математическую экспедицию под девизом «Добывай знания сам». Сначала проверим, готовы ли мы к путешествию. Ведь, чтобы новых знаний набраться, нужно на старые опираться!
У вас на партах лежат оценочные листы (Приложение 1). Подпишите их. За каждый пройденный этап вы будете выставлять себе баллы. А в конце урока мы выставим отметку за работу на уроке.
II Проверка домашнего задания
Учащиеся проверяют правильность выполнения домашнего задания, сверяя ответы. Выставляют баллы в оценочный лист. Максимально – 7 баллов.
III Операционно-познавательный этап
Формируемые компетенции: контроль, коррекция, самооценка.
1 Прочтите дроби:
Учащиеся фронтально читают дроби, называют числитель и знаменатель дроби, что показывает знаменатель дроби и числитель дроби.
Что вы можете сказать о данных дробях? (правильные, неправильные, сократимые).
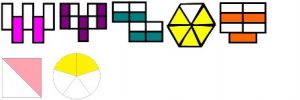
2 Определите, какая часть фигуры закрашена?
Учащиеся называют дробь и для самопроверки на интерактивной доске открывают ответ.
3 Посмотрим, ребята, какой багаж знаний возьмет в дорогу каждый из вас.
У вас на столах лежат путевые листы с заданиями. Нужно определить, какая часть каждой фигуры закрашена красным, какая зеленым, какая часть красным и зеленым вместе, а какая желтым. Заполнить таблицу.
Класс выполняет самостоятельную работу на листах. (Приложение 2). Для проверки обмениваются тетрадями с соседом по парте.
Итак, проверим, что каждый из вас возьмет в путь.
Учащиеся выполняют взаимопроверку теста (ответы на слайде).
Сколько ответов верно, такая оценка и ставится в оценочный лист. Максимально – 8 баллов.
4 Посмотрите на изображение. На координатном луче расставлены дроби.
Вы уже знаете, что правильные дроби размещены правее 1, а неправильные левее.
III Постановка проблемы
— Какие умения, навыки при изучении дробей вы приобрели?
Читать, записывать, изображать на числовом луче одну или несколько равных долей целого.
На экране изображены дроби:
На какие группы их можно разбить?
Разбейте дроби на две группы.
Ребята, могли бы вы назвать из записанных дробей самую маленькую, самую большую; расставить дроби в порядке возрастания?
Сомневаетесь? Значит, вам не всё ещё известно о дробях. Сформулируйте возникшую проблему.
Как сравнить обыкновенные дроби?
Тогда сформулируем тему урока: «Сравнение дробей».
Сформулируйте цель урока.
Учиться сравнивать обыкновенные дроби.
Записываем тему урока.
IV Этап формирования новых знаний
Формируемые компетенции:
1 умение принимать и понимать учебную задачу;
2 построение речевого высказывания в устной и письменной формах;
3 использование знаково-символических средств.
У вас на партах лежат два равных прямоугольника, разделённых на 8 частей. Заштрихуйте на одном прямоугольнике 4 части, а на другом 5 частей Заштрихованные части сравнить.
Практическая работа (по парам).
Сделать вывод.
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравните свой вывод с выводом в учебнике на стр. 33.
Работа с учебником.
Сравните дроби:
Учащиеся используют правило для сравнения дробей, записывают дроби в тетради, сравнивают, а затем выходят к доске по одному и ставят знак неравенства.
Друзья разделили две шоколадки так: одну на 6 частей, другую на 12 частей. Что больше?
Заштрихуйте на одной шоколадке 2 части, а на другой 4 части. Заштрихованные части сравните.
Практическая работа (по парам).
Сделайте вывод.
Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.
Сравните свой вывод с выводом в учебнике на стр. 33
Работа с учебником.
Сформулируйте правило сравнения дробей с одинаковыми числителями.
Учащиеся формулируют правило.
Сравните дроби:
V Физкульминутка
VI Закрепление изученного материала
Формируемые компетенции:
1 планирование своих действий в соответствии с поставленной задачей и условиями её реализации;
2 осуществление итогового и пошагового контроля;
3 выполнение учебных действий в материализованной и умственной форме;
4 умение точно формулировать обоснование выбора способа деятельности.
У каждого футболиста на майке написан номер. Но тренер перепутал все футболки, и их надо расположить по убыванию номеров. Давайте поможем тренеру. Подумайте. Сравните. В результате должно получиться слово.
Расположить дроби в порядке убывания.
Учащиеся по одному выходят к доске и расставляют человечков.
По одному баллу выставляется за правильный ответ.
Работа с учебником. Выполнить № 86 а.
— Каким правилом пользовались?
Выполнить № 89 а,б.
Выполняют работу в тетрадях. Проверяют самостоятельно.
Баллы выставляются в лист самооценки. Максимально — 8 баллов.
VII Контрольно-оценочный этап
Формируемые компетенции:
1 осуществление наблюдения за своей учебной деятельностью;
2 самоанализ учебной деятельности;
3 выполнение учебных действий в материализованной и умственной форме;
4 осуществление самооценки и самокоррекции.
Наше математическое путешествие подходит к концу. Мы стоим у подножия высокой горы, название которой «Дроби». Нам предстоит трудное восхождение. Для того, чтобы проверить как мы научились сравнивать дроби с одинаковыми знаменателями и дроби с одинаковыми числителями, проведем мини-тестирование (Приложение 3).
Работу выполняют самостоятельно. Правильность выполнения проверяется с помощью таблиц на экране. Оценку учащиеся ставят в оценочный лист.
VIII Коррекционный этап
— Что сегодня нового вы узнали на уроке?
– Какую цель ставили в начале урока?
– Цель достигнута?
Ответы учащихся.
В конце путешествия наш багаж пополнился ещё одним знанием — «Сравнением дробей»
Вы уже знаете и умеете сравнивать дроби.
Теперь оцените свою работу на уроке.
Посчитайте, сколько у вас всего баллов, а затем поставьте отметку.
Учащиеся выставляют отметку за урок.
IX Домашнее задание
Полученные на уроке знания вам пригодятся для выполнения домашнего задания. Записывайте: п. 4, № 101, 103.
Учащиеся записывают в дневники домашнее задание.
Задача про торт «Прага». Найдите вес каждого ингредиента в граммах (Приложение 4).
Л.Н. Толстой сравнивал человека с дробью. Перефразируя его слова можно сказать, что человек подобен дроби, числитель – это хорошее, что о нём говорят и думают люди, а знаменатель – это то, что думает он о себе сам. Известное правило – чем больше числитель, тем больше дробь, верно не только в математике, но и в жизни.





 Предложить публикацию
Предложить публикацию