Надежда ГОРДЕЙЧУК,
учитель математики
ГУО «Гимназия № 1 имени Ф.Я.Перца г. Пинска»,
Брестская область
nadezdagord07@gmail.com
Хорошо известно, что одним из главных условий осуществления деятельности, достижения определенных целей в любой области является мотивация. А в основе мотивации лежат, как говорят психологи, потребности и интересы личности. Следовательно, чтобы добиться хороших успехов в учебе школьников, необходимо сделать обучение желанным процессом. Вспомним, что французский писатель Анатоль Франс отмечал: «Лучше усваиваются те знания, которые поглощаются с аппетитом».
Интересный урок можно создать за счет следующих условий:
– личности учителя (очень часто даже скучный материал, объясняемый любимым учителем, хорошо усваивается);
– содержания учебного материала (когда ребенку просто нравится содержание данного предмета);
– методов и приемов обучения.
Если первые два пункта не всегда в нашей власти, то последний – поле для творческой деятельности любого преподавателя.
С позиций современной педагогической науки следует обратить внимание на следующее:
– по возможности обратиться к каждому ученику несколько раз, то есть осуществлять «обратную связь» – корректировать непонятое или неправильно понятое;
– ставить отметку ученику не за отдельный ответ, а за несколько (на разных этапах урока);
– постоянно и целенаправленно заниматься развитием качеств, лежащих в основе развития познавательных способностей: быстрота реакции, все виды памяти, внимание, воображение, ведь основная задача учителя – развить мышление ребенка средствами своего предмета;
– стараться, когда возможно, интегрировать задания, связывая темы своего предмета с другими учебными дисциплинами, обогащая знания, расширяя кругозор учащихся.
Для этого надо вводить в процесс обучения развивающие приемы, повышающие интерес к предмету, а, следовательно, и активность детей. Что же это за приемы? Приведем некоторые примеры.
1 Разминки
Это прием фронтальной работы, вовлекающий в деятельность весь класс, развивает быстроту реакции, умение слушать и слышать вопрос, четко и конкретно мыслить. Разминка занимает 5–7 минут. Этот вид работы проводится на этапе проверки домашнего задания или этапе первичного усвоения, когда вопросы просты (репродуктивные) и требуют однозначного, быстрого ответа. Детям предлагается как можно быстрее, можно хором, отвечать на вопросы (их обычно 15–20) и самостоятельно оценивать себя: в случае правильного ответа делать в тетради заметку, ставить «+».
Примеры вопросов:
— Назовите наименьшее однозначное число.
— Сколько человек в трех квартетах?
— Чему равна сумма чисел, на которые показывают стрелки механических часов в 9 утра?
— Сколько ступенек у лестницы, если средняя – 8-я ступенька?
2 Буквенный диктант
Его можно использовать перед объяснением новой темы. Не учитель называет тему, а ученики. Смысл диктанта в следующем: учащиеся отвечают про себя на вопрос, а записывают лишь первую букву ответа. Затем из выделенных букв составляют слово.
О – суша посреди моря (остров);
П – параллелограмм, у которого диагонали равны (прямоугольник);
З – утренняя трапеза (завтрак);
А – домашний бассейн для рыб (аквариум);
Е – детский юмористический журнал (Ералаш);
К – английский писатель, которому обязан своей всемирной известностью Маугли (Киплинг);
А – математическое предложение, принимаемое без доказательства (аксиома);
Ь – буква, превращающая геометрическую фигуру в топливо (угол – уголь)
Л – царствующая особа из земноводных (лягушка);
Т – четырехугольник, у которого только две противоположные стороны параллельны (трапеция).
Ответ: показатель.
При использовании приема «Буквенный диктант» вопросы формулируются из соответствующей темы по математике, из любых предметов школьного курса.
3 Цифровой диктант
Эффективно используется для быстрой проверки усвоения и закрепления знаний. Учитель произносит некоторое утверждение и, если ученик согласен, то он ставит единицу (1), если нет – нуль (0). В результате получается число. Все, кто получил правильное число, получают балл за данный этап урока.
Пример.
Тема «Решение уравнений» (5-й класс)
1) Уравнение – это равенство, содержащее букву, значение которой надо найти. (1)
2) Чтобы найти неизвестное слагаемое, надо к сумме прибавить известное слагаемое. (0)
3) Решить уравнение – это значит найти все его корни (или убедиться, что корней нет). (1)
4) Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое. (1)
5) 120 больше 60 на 2. (0)
Ответ: 10 110.
Подобные диктанты с большим удовольствием составляют сами учащиеся и подбирают вопросы из многих учебных предметов.
4 Задания со сменой установки
Этот прием работы на уроке позволяет не только проверить знания детей по теме, но и развивать зрительную память, быстроту реакции, внимание.
Суть приема в следующем: на доске заранее пишется задание (несколько чисел, фигуры), учащимся предлагается их запомнить в том же порядке. Затем задание убираем, а дети должны постараться ответить на вопросы учителя письменно в тетрадях.
Пример.
25; 16; 8; 10; 13
1) Сколько было четных чисел? (три)
2) Сколько чисел делятся на 5 без остатка? (два)
3) Результат деления второго числа на третье? (два)
5 Вместо правил – ассоциация
Некоторым учащимся тяжело усвоить правила или определения, а, выучив их, трудно применить при выполнении тех или иных заданий. Гораздо легче усваивается ход решения, если некоторые его моменты связаны с жизнью, этапы решения сравниваются с понятиями окружающего нас мира. В этом случае математические умозаключения ассоциируются с представлениями реальной действительности, либо зрительная ассоциация.
Примеры.
1) При изучении темы «Нахождение дроби от числа» и «Числа по его дроби» предлагаю учащимся присмотреться к записи: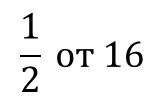 
Предлог «от» начинается с буквы «о». Если посмотреть на нее издалека, то увидишь точку (о – ∙), то есть знак умножения. Значит, число нужно умножить на дробь. В случае
внимание следует обратить на слово «это», в первой букве которого «спрятан» знак деления на концах э, следовательно, число дели на дробь. В этих объяснениях используется ассоциация букв со словами действий.
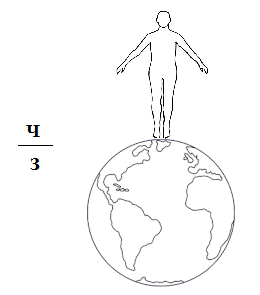
2) Нередко учащиеся путают, где в дроби находится числитель, а где знаменатель (сами слова). Можно предложить следующую ассоциацию: говорим о том, что Человек стоит на Земле, а не наоборот.
3) При прохождении темы «Неравенства» учащиеся путают, когда на схематичном рисунке пустая точка, когда закрашенная. Здесь я предлагаю следующую ассоциацию: здесь знак неравенства – это клюв цыпленка. Видит перед собой сухую, пустую горошину – закрыл клюв (при строгом знаке – точка не закрашена). Увидел сочную – открыл клюв (нестрогий знак – точка закрашена).
Ребята, которым темы объяснены с применением ассоциации, гораздо лучше усваивают материал.
6 Контрпримеры
Нередко на уроке можно услышать, как ученик, не разобравшись в определении, изменяет его. Чаще изменяется какое-то условие, признак.
Задача состоит в том, чтобы обратить внимание учащихся на упущенное слово, разъяснить его значение, показать к каким последствиям приводит изменение. Для этого я составляю «новые» определения и предлагаю учащимся в классной или домашней работе подыскать к ним контрпримеры.
Пример.
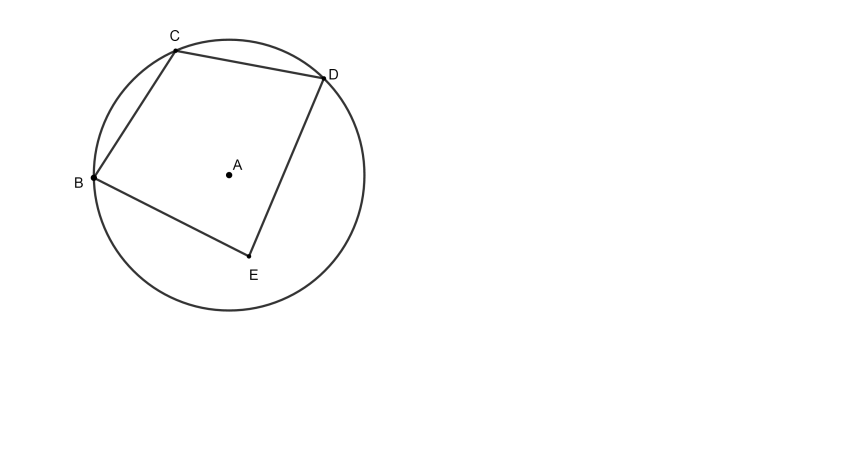
В определении вписанного в окружность многоугольника пропускаю слово «все».
Получаем: «Вписанным в окружность называется многоугольник, (…) вершины которого лежат на окружности»
Контрпример:
7 Интеллектуальные игры
Наряду с традиционными методами, использую обучающие игры, потому что во время игры у учащихся развиваются такие качества, как готовность к сотрудничеству, взаимопомощь, способность к решению проблем, коммуникабельность. Для успешного проведения игры с математическим содержанием учителю необходимо определить место игры в системе других видов деятельности на уроке, целесообразность использования на разных этапах изучения материала, учитывать уровень подготовки учащихся.
8 Простой прием в непростых задачах
Учащихся старших классов увлекают задачи с нестандартным решением, задачи с изюминкой. Приведу примеры таких заданий.
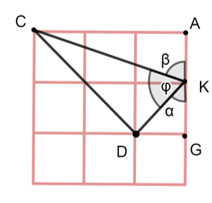
1) Вычислить: arctg1+arctg2+arctg3 (геометрический метод решения алгебраической задачи)
∠DKG=α=arctg1;
∠CKD=φ=arctg2;
∠AKC=β=arctg3;
arctg1+arctg2+arctg3=α+φ+β=π.
Ответ: π.
9 Составление опорных схем, практические работы
Примеры.
1) Дорисуйте всю веточку, при условии, что на рисунке изображена
часть веточки с одинаковыми листочками.
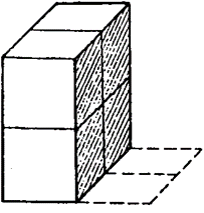
2) Ребята хотели построить большой кубик из нескольких маленьких.
Они построили только
часть большого кубика и истратили маленьких кубиков столько, сколько их показано на рисунке.
Сколько всего кубиков им придется израсходовать, чтобы завершить свою конструкцию?
10 Решение практико-ориентированных задач
Пример.
Виктору необходимо приобрести новый телевизор стоимостью 900 рублей взамен сломавшегося. Поскольку покупка для Виктора оказалась незапланированной, то для того чтобы не нарушать другие свои планы, он решил воспользоваться кредитом. Виктор рассматривает два предложения:
а) В магазине предлагают кредит на следующих условиях: при покупке Виктор платит 90 рублей в качестве первоначального взноса, а затем каждый месяц в течение года еще по 90 рублей.
б) Виктор может взять кредит в банке. Если брать кредит на один год, то процентная ставка составит 13,2 % на всю сумму задолженности.
Какое предложение (а или б) должен принять Виктор, если он хочет заплатить меньше денег? Ответ обоснуйте (республиканская работа по финансовой грамотности 2020/2021 учебный год).
11 Занимательные задачи
«На поверхности озера, посещаемого стаями фламинго и журавлей, плавает лотос, стебель которого на пол-локтя поднимается над водой. Гонимый ветром, стебель постепенно наклоняется, погружается в воду и в конце концов совсем исчезает под водой на расстоянии двух локтей от того места, где и вырос. Подсчитай, о мудрый математик, глубину озера.»
Ответ:
Интерес к математике формируется с помощью не только математических игр, занимательных задач, разгадывания головоломок, но и логической занимательностью самого материала: проблемным изложением, постановкой гипотез, рассмотрением различных путей решения проблемной ситуации, решением задач или доказательством теорем различными способами.
Неотъемлемой частью формирования устойчивого познавательного интереса к изучению математики является участие ребят в научно-практических конференциях, неделе математики. Учащиеся вовлекаются в активную мыслительную деятельность, формируется осознанный подход при изучении учебного предмета.
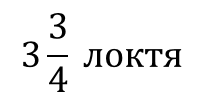
Предложить публикацию