Введение централизованного экзамена в 11-м классе вызывает необходимость изменения в выборах методов и форм работы учителя. Это обусловлено тем, что в заданиях изменилась формулировка вопросов: вопросы стали нестандартными, часто задаются в косвенной форме, ответы на вопросы требуют детального анализа условия задачи.
Галина ГЛЯК,
учитель математики
ГУО «Средняя школа № 17 г. Орши»,
Витебская область
При подготовке учащихся к сдаче экзамена по математике перед каждым учителем, работающем в 11-х классах, стоят вопросы: «Как подготовить выпускников к успешной сдаче ЦЭ или ЦТ? Где взять время на организацию повторения?» Путей решения несколько:
– организация факультативных занятий;
– организация дополнительных занятий (поддерживающие занятия, дополнительные занятия на платной основе);
– уроки повторения.
Но, как показывает практика, учащиеся в силу своей загруженности не всегда могут посещать дополнительные занятия, количество часов, выделенное на повторение, недостаточно, чтобы успешно повторить весь материал.
Введение централизованного экзамена в 11-м классе вызывает необходимость изменения в выборах методов и форм работы учителя. Это обусловлено тем, что в заданиях изменилась формулировка вопросов: вопросы стали нестандартными, часто задаются в косвенной форме, ответы на вопросы требуют детального анализа условия задачи. Содержание задач содержит математические тонкости, на отработку которых в учебной программе отводится недостаточное количество часов. В задания включаются вопросы, которые изучались в 5–6-х классах, либо на их изучение отводилось небольшое количество времени (проценты, пропорции, свойства числовых неравенств, стандартный вид числа, чтение графиков функций и т.д.).
Для успешного повторения учителю необходимо выполнять ряд условий:
– повторение должно быть организовано на протяжении всего учебного года;
– повторение необходимо планировать и тщательно отбирать материал для него;
– материал для повторения должен быть правильно дозирован и распределен во времени;
– сочетание отдельных видов повторения должно быть органически связано и продумано;
– в процессе повторения необходимо стимулировать самостоятельность и активность учащихся.
Рассмотрим пути решения проблемы на примере темы «Числа и вычисления».
Первый вопрос: «С чего начать работу?» Конечно же, с документов, регламентирующих выпускные экзамены по математике. В частности, «Спецификация экзаменационной (тестовой работы) по учебному предмету «Математика» для проведения централизованного экзамена и централизованного тестирования в 2024 году».
В структуру теста включены только четыре задания на тему «Числа и вычисления». Однако мы все прекрасно понимаем, что доскональное знание данного раздела является базовым практически во всех заданиях.
На сайте РИКЗ размещены статьи (https://rikc.by/20-stati.html) с анализом выполнения всех заданий в соответствии с разделами программного материала по которому разрабатываются тесты, рассматриваются ошибки, допущенные абитуриентами на ЦТ и ЦЭ начиная с 2018 года.
Зачастую вычислительные ошибки являются одной из причин неверного выполнения заданий. При правильном построении рассуждений, зная алгоритмы решения, учащиеся довольно часто ошибаются именно при выполнении вычислений, что свидетельствует о недостаточно сформированном умении осуществлять проверку полученных в ходе решения результатов. Немаловажным для успешного решения задачи является работа с ее условием, которое требует внимательного и осознанного прочтения.
Изучение данных статей учителем дает представление об общих моментах, на которые при повторении тем, да и при изучении нового материала, стоит сделать акцент и обратить внимание учащихся.
Учиться на чужих ошибках хорошо, но при подготовке к ЦЭ или ЦТ – лучше на своих.
Повторение каждой темы можно выстраивать по следующему алгоритму:
– теоретический блок по теме;
– разбор основных типовых задач;
– тренировочные упражнения (Приложение 1);
– работа над типичными ошибками, индивидуальные консультации;
– контроль знаний (Приложение 2).
Этот алгоритм хорошо работает на уроках повторения, но количества часов недостаточно, чтобы реализовать его по всем темам в конце учебного года. Разбив его на части, можно реализовать в течение нескольких уроков. Где взять время? Один из путей разрешения проблемы – система устных упражнений.
Сегодня существует очень много дидактических и методических пособий для организации работы с устными упражнениями, но чаще всего они рассчитаны на организацию поурочного устного счета по классам и содержат большой объем материала. Что использовать и в каком объеме? Как организовать сам процесс? Ведь устный счет – это только этап урока и его продолжительность не должна превышать 10 минут, в лучшем случае 7–8 минут.
Для организации эффективной работы с устными упражнениями необходимо, чтобы задачи были заранее выписаны на доске или отдельных листах, чтобы каждый учащийся видел их на протяжении всего процесса устного решения.
Однако не стоит забывать, что устные задачи необходимо чередовать с письменным выполнением упражнений. Если это условие нарушается, то многие учащиеся через какое-то время не смогут успешно справиться с аналогичными задачами.
Часто учитель работает на параллели и у него несколько выпускных классов. Все классы разные: по темпераменту, способностям и возможностям. Иногда то, что легко осиливают учащиеся одного класса, не под силу учащимся другого. То есть возникает необходимость в подготовке нескольких различных вариантах заданий. Таким образом возникает необходимость создания электронного банка заданий, чтобы при небольших затратах времени можно было сформировать различные карточки для организации повторения с учетом возможностей и способностей учащихся каждого класса.
На уроках для повторения я использую несколько приемов, способствующих активизации воспроизведения и запоминания математических терминов и понятий:
– вставить в предложение пропущенное слово – такие задания легко формируются из текста теоретического материала учебника (Приложение 3);
– сформулировать теорему, определение, правило – такие задания включаю в устный опрос, математические диктанты (Приложение 4);
– выбрать верное утверждение, формулу;
– разгадать кроссворд;
– составить кроссворд – для организации этого вида работы использую заранее подготовленный словарь терминов и понятий по теме.
Работа над теоретическим материалом длится на протяжении 1–2 уроков. Далее идет закрепление практических умений с использованием устных заданий. Каждое задание может быть представлено в нескольких вариантах, это дает возможность индивидуализировать процесс повторения. В завершение проводится математический диктант или тест.
Если проанализировать программный материал, предложенный в Спецификации в разделе «Числа и вычисления», то можно заметить, что более чем на половину он содержит вопросы из курса математики 5–6-го классов, то есть то, что изучали давно. Материал, предложенный в конце учебного пособия «Алгебра 11», по данному разделу не дает возможность повторить вид числа, наибольший общий делитель, наименьшее общее кратное, проценты. Выход? Материалы, размещенные на сайте Единого информационно-образовательного ресурса (https://eior.by/obrazovanie/obshchee-srednee). Тесты, которые там предложены, можно брать в полном объеме или формировать из нескольких. Для организации повторения подойдут тесты всех классов.
Для менее подготовленных учащихся я использую обыкновенные тренажеры, алгоритмы, показываю приемы быстрого счета.
Например, можно показать учащимся способ нахождения приближенного значения квадратного корня из числа х, которым пользовались еще древние вавилоняне. Число х они представляли в виде суммы а2+b, где а2 ближайший к числу х точный квадрат натурального числа а, и пользовались формулой
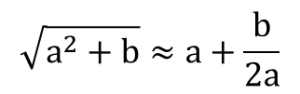
Время, которое стоит потратить на отработку вычислительных навыков, каждый учитель определяет самостоятельно, но не стоит ее прекращать на протяжении всего учебного года. Осуществлять это можно без больших временных затрат, достаточно дополнить выполняемые задания дополнительными вопросами.
Например, учащийся решил уравнение. Обсудите получившиеся корни:
– дайте характеристику чисел, которые получились в результате решения;
– являются ли корни взаимно обратными, взаимно простыми, противоположными числами (ответ объясните);
– возведите в степень сумму корней уравнения;
– извлеките квадратный корень из произведения корней уравнения;
– на сколько процентов первый корень больше, чем второй;
– сколько процентов первый корень составляет от второго;
– запишите корень в виде суммы разрядных слагаемых;
– представить частное корней в стандартном виде;
– представьте меньший корень в виде логарифма с основанием а и т.д.
При решении неравенств, систем и совокупностей неравенств добавьте в условие:
– нахождение наименьшего или наибольшего целого, натурального, целого отрицательного числа из множества решения;
– определение количества целых, целых отрицательных или натуральных чисел на определенном промежутке;
– нахождение произведения наибольшего и наименьшего решения и т.д.
При нахождении градусной меры угла, дуги ответ можно предложить записать в радианах и наоборот, найти соответствующее значения синуса, косинуса, тангенса, котангенса данного угла. При вычислениях значений выражений можно предложить учащимся найти арксинус, арккосинус, арктангенс или арккотангенс этого числа.
Времени данные задания занимают не много, а многократное повторение способствует запоминанию.
Открытый банк тестовых материалов по математике, размещенный на сайте РИКЗ, рекомендуется учащимся старших классов, абитуриентам для самостоятельной подготовки к централизованному экзамену и централизованному тестированию, а также педагогическим работникам учреждений общего среднего образования. Эти материалы я использую для составления итоговых тестов. Набор упражнений дает возможность составления двух вариантов тестов. (https://rikc.by/otkrytyj-bank-testovyh-materialov/658-matematika.html).
В заключение хочу отметить, что с помощью устных упражнений и тестовых заданий учитель за короткий промежуток времени может организовать повторение ранее изученного материала, осуществить корректировку знаний и умений учащихся.









 Предложить публикацию
Предложить публикацию