Алла ЛУКАШЁНОК,
учитель математики, учитель-методист
ГУО «Шайтеровская средняя школа Верхнедвинского района»,
Витебская область
Форма урока: игра «Лабиринт».
Тип урока: практикум по решению задач.
Применяемые формы обучения: групповая, индивидуальная.
Методы и приёмы обучения: познавательная игра, мозговой штурм, самоконтроль, взаимоконтроль.
Цель урока: обобщение, закрепление и углубление знаний и умений учащихся по теме «Проценты» с опорой на практическую направленность познавательной деятельности обучающихся и на практико-ориентированные задания.
Задачи личностного развития и воспитания:
– содействовать формированию у учащихся функциональной грамотности через отбор содержания дидактического материала;
– способствовать повышению мотивации учащихся, нацеленности их на успех в учебной деятельности с помощью организации системы контроля и учёта индивидуальных и командных достижений;
– создать условия для формирования у учащихся самостоятельности, ответственности, развития коммуникативных и рефлексивных способностей.
Оборудование и материалы: карта-схема этапов игры (на классной доске), флажки на магнитах для обозначения местонахождения команд, разноуровневые практико-ориентированные и нестандартные задания для прохождения «лабиринта», жетоны для учёта индивидуальных и командных достижений, грамота для команды-победителя.
Ход урока
1 Организационно-мотивационный этап (3 мин.)
Задача этапа
Создать условия для организации внимания, определения учащимися темы и принятия целей урока.
Содержание
Определение учащимися темы урока (загадка):
На рубль – копейки,
На доллары – центы,
Бегут-набегают в банке … проценты
Сообщение учителем и принятие учащимися целей и задач урока, организация деления учащихся на команды, сообщение правил игры.
2 Операционно-познавательный этап
2.1 Вход в лабиринт (7 мин.)
Задача этапа
Организовать повторение теоретического материала (знак «процент»; определение процента; соответствие между процентом и его записью в виде дроби и обратно, частные случаи – 50% – половина, 25 % – четверть; алгоритмы решения задач на проценты).
Содержание
Команды получают тестовые задания 1-2 уровней сложности на знание теоретического материала темы с выбором варианта ответа (Приложение 1). Учитель выступает в роли ведущего (задаёт вопросы, определяет правильность ответа, за каждый верный ответ выдает жетон (командный и (или) индивидуальный) с цифрой «1», осуществляет промежуточную рефлексию).
Формируемые компетенции
Развитие способностей использовать усвоенные теоретические знания, понимать противоречия в тексте, анализировать информацию (математическая грамотность, читательская грамотность), работать в команде.
2.2 Лото «Ключевые задачи на проценты» (10 мин.)
Задачи этапа
Создать условия для диагностики владения учащимися алгоритмом выбора вида ключевой задачи; закрепления навыков решения задач; формирования умений моделирования; развития коммуникативных и рефлексивных способностей.
Содержание
Выполняются тренировочные упражнения на установление соответствия между предложенным заданием и видом ключевой задачи (Приложение 2).
1) Учащимся предлагается распределить задачи по ячейкам лото «Нахождение процентов от величины», «Нахождение величины по её процентам», «Выражение процентного соотношения одного числа от другого». Жетоны с цифрой «2» (2-й уровень усвоения учебного материала). Промежуточная рефлексия.
2) Составить выражения для решения предложенных задач. Выдача командных и индивидуальных жетонов с цифрой «3» (3-й уровень). Промежуточная рефлексия.
3) Моделирование ключевых задач. Учащимся предлагается рассмотреть задачу на нахождение процентов от величины и изменить её условие так, чтобы получить задачи на нахождение величины по её процентам и процентного соотношения одного числа от другого. Жетоны с цифрой «4».
Формируемые компетенции
Математическая грамотность – применение методов математического моделирования (сравнение, классификация, систематизация, анализ и синтез, интерпретация).
2.3 Мозговой штурм «Решение задач на проценты» (10 мин.)
Задачи этапа
Способствовать формированию у учащихся математической и финансовой грамотности, развитию умений и навыков самоанализа, самоконтроля и взаимоконтроля, коммуникативных способностей.
Содержание
Решение учащимися разноуровневых практико-ориентированных заданий, нацеленных на формирование математической и финансовой грамотности с акцентом на рекламу белорусских товаров и услуг (Приложение 3). Самостоятельное чередование учащимися индивидуальной и групповой работы (команды могут применять «мозговой штурм», но по времени выигрывает обычно та команда, где вначале каждый качественно поработал над своим вопросом, не перекладывая его на других). Учитель отмечает жетонами организацию работы в команде и личный вклад каждого. При необходимости команда обращается за помощью к учителю, уплатив «штраф» жетонами в размере 50 % от уровня задания.
Формируемые компетенции
Умение принимать и понимать учебную задачу, осуществлять анализ объектов с выделением существенных и несущественных признаков, выполнять алгоритмические предписания, осуществлять пошаговый контроль, самоконтроль, взаимоконтроль и коррекцию сформированных умений, навыков и способов деятельности.
2.4 «Заморочки из бочки» (10 мин.)
Задача этапа
Содействовать развитию способности применять знания, умения и навыки в разнообразных контекстах, видах деятельности, при решении практико-ориентированных задач, задач с межпредметным содержанием.
Содержание
В бочке – 4 «заморочки», содержащих задания интегрированного характера (Приложение 4). Жетоны с цифрой «5».
Формируемые компетенции
Умение упрощать и конкретизировать ситуацию; перевести на математический язык реальную ситуацию; выбрать модель для решения задачи.
3 Выход из лабиринта (5 мин.)
Задача этапа
Способствовать развитию у учащихся рефлексивных способностей.
Содержание
Что вы узнали на уроке? Какие затруднения испытывали? Как их преодолевали?
Оценка учащимися результатов их деятельности в процессе урока.
Анализ урока учителем, подведение итогов.
Приложение 1
Тестовые задания на знание теоретического материала по теме «Проценты»
1 Каким знаком можно заменить слово «процент»?
А) 0\0; Б) 0//0; В) %; Г) 0/00; Д) 00/0.
2 Укажите неправильное равенство:
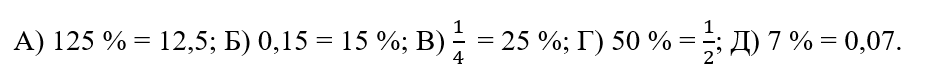
3 Укажите верные утверждения:
А) процентом называется сотая доля числа;
Б) если увеличить число на 50 %, то число увеличится в 2 раза;
В) чтобы найти, сколько процентов составляет число а от числа b, нужно число а разделить на число b и выразить это отношение в процентах;
Г) чтобы найти несколько процентов данного числа, можно выразить проценты в виде десятичной дроби и разделить число на эту дробь;
Д) если число а уменьшить на 20 %, то получится 0,8 а;
Е) чтобы найти число по его процентам, можно выразить проценты в виде дроби и умножить данную его часть на эту дробь;
Ж) чтобы узнать, на сколько процентов число a больше числа b, нужно вычислить
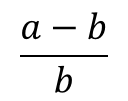
З) если цену на товар сначала понизить на 25 %, а затем повысить на 25 %, то новая цена будет равна первоначальной;
И) для решения задачи «В бидон налили 4 л молока трехпроцентной жирности и 6 л молока шестипроцентной жирности. Сколько процентов составляет жирность молока в бидоне?» необходимо найти значение выражения:
![]()
Ключ-ответ: 1 В; 2 А; 3 А, В, Д, И.
Приложение 2
Лото «Ключевые задачи»

1) Распределите по ячейкам лото задачи:
– Телефон, который стоил 4500 рублей, купили со скидкой 15 %. Сколько заплатили за телефон? (3825 руб.)
– Телефон купили со скидкой 15 % и заплатили 3825 рублей. Какова первоначальная цена телефона? (4500 руб.)
– Телефон стоил 4500 рублей, а затем, с учётом скидок, стал стоить 3825 рублей. На сколько процентов снизилась цена? (на 15%)
2) Составьте выражения для решения предложенных задач и заполните вторую строку таблицы.
3) За стиральную машину Атлант и её установку заплатили 1840 рублей. Стоимость установки составляет 12 % от стоимости машины. Сколько стоит машина? (1619,2 руб.) Измените условие задачи так, чтобы получились задачи на нахождение величины по её процентам и нахождение процентного соотношения одного числа от другого. Заполните третью строку ячеек лото.
Приложение 3
Мозговой штурм
Решение задач на проценты
1) Социальная скидка на лекарственные препараты в Беларуси в сети аптек «Остров Здоровья» составляет 5 %. Лекарственное средство стоит 234 руб. 67 коп. Определите сумму скидки в рублях.
2) Бабушке прибавили пенсию. В СМИ говорилось, что пенсия поднимется на 10 %. Проверьте, соответствует ли это действительности, если первоначально пенсия бабушки была 800 рублей, а прибавка составила 80 рублей.
3) Национальный банк Республики Беларусь начисляет на срочный вклад 20 % годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через 2 года, если никаких операций со счетом проводиться не будет?
4) Морская вода содержит 5 % соли. Сколько килограммов пресной воды надо прибавить к 40 кг морской воды, чтобы содержание соли в ней составило 2 %?
5) Семье белочек на зиму требуется 350 г сухих грибов. Известно, что в сырых грибах 85 % воды, в сухих грибах 67 % воды. Сколько граммов сырых грибов нужно собрать белочкам?
Приложение 4
Задания для гейма «Заморочки из бочки»
1) «В начале одного из сезонов мне неожиданно сообщили, что я должен буду заплатить за снятые помещения почти в три раза больше, чем прежде. На следующий день я получил письмо, извещающее меня, что арендная плата будет увеличена только на пятьдесят процентов, а не на триста процентов» (Д. Карнеги. «Как завоёвывать друзей и оказывать влияние на людей»). Найдите математическую ошибку в этом тексте.
2) Проценты применяются в медицине, в агрономии, в программировании, в кулинарии, в статистике, в прогнозировании, в физике, в химии, в метеорологии, в технике, в торговле, в составах тканей и анализе деятельности, на выборах, при всевозможных банковских операциях, в расчётах тарифов на коммунальные услуги и при начислении зарплаты и налогов. А где не применяются проценты?
3) Освейское озеро находится на территории Верхнедвинского района Витебской области, входит в состав Освейского ландшафтного заказника республиканского значения и является вторым по площади озером в Республике Беларусь. В Освейское озеро впадает река Выдринка. Укажите, сколько процентов составляет объём воды, поступившей в Освейское озеро из реки Выдринка за 6 часов, от объёма воды, поступившей за 3 часа?
4) Вера и Аня посещают математический кружок, в котором больше 91 % мальчиков. Найдите наименьшее возможное количество участников кружка.



 Предложить публикацию
Предложить публикацию